摘要：5．理解分式的有关概念及其基本性质.掌握分式的加.减.乘.除运算法则.通过类比整式的运算.进一步体验类比思想和化归思想
网址：http://m.1010jiajiao.com/timu3_id_486549[举报]
圆的有关概念：
（1）圆两种定义方式：
（a）在一个平面内线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做
（b）圆是所有点到定点O的距离
（2）弦：连接圆上任意两点的
（3）弧：圆上任意两点间的部分叫
（4）等弧：在同圆与等圆中，能够
（5）等圆：能够
查看习题详情和答案>>
（1）圆两种定义方式：
（a）在一个平面内线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做
圆心
圆心
．线段OA叫做半径
半径
．（b）圆是所有点到定点O的距离
等于
等于
定长r的点的集合．（2）弦：连接圆上任意两点的
线段
线段
叫做弦．（弦不一定是直径，直径一定是弦，直径是圆中最长的弦）；（3）弧：圆上任意两点间的部分叫
弧
弧
（弧的度数等于这条弧所对的圆心角的度数，等于这条弧所对圆周角的两倍）（4）等弧：在同圆与等圆中，能够
完全重合
完全重合
的弧叫等弧．（5）等圆：能够
完全重合
完全重合
的两个圆叫等圆，半径相等
相等
的两个圆也叫等圆..阅读理解题：
我们学习了二次根式的概念及其基本性质，又学习了二次根式的乘法运算法则，下面我们再来思考下面的问题：
（1）计算：
•
=
•
=
•
=
=
=
．
试一试：化简：①
=
=
；②
=
=
；
（2）计算：（2﹢
）（2-
）=
﹢
）（
-
）=
-3）（
+3
+3）使其结果不再含有根号；同样请你仿照（1）的方法将下列二次根式化简：
．
查看习题详情和答案>>
我们学习了二次根式的概念及其基本性质，又学习了二次根式的乘法运算法则，下面我们再来思考下面的问题：
（1）计算：
| 2 |
| 2 |
2
2
；| 3 |
| 3 |
3
3
；| 12 |
| 3 |
6
6
；显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号．因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号，使分母中不再含有根号，如：
| ||
|
| ||||
|
| ||
| 3 |
试一试：化简：①
| 1 | ||
|
1•
| ||||
|
1•
| ||||
|
| ||
| 6 |
| ||
| 6 |
| ||
|
| ||||
|
| ||||
|
| ||
| 3 |
| ||
| 3 |
（2）计算：（2﹢
| 3 |
| 3 |
1
1
；（| 6 |
| 2 |
| 6 |
| 2 |
4
4
；同样发现相乘的积不再含有根号．想一想：（| 7 |
| 7 |
| 7 |
| 1 | ||
|
•
•
•
=
=
．
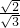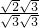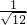=______=______；②
=______=______；
﹢
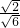-3）（______）使其结果不再含有根号；同样请你仿照（1）的方法将下列二次根式化简：
．