摘要:解:反比例函数的图象是双曲线.因为k=-5<0.所以图象在第二.四象限.故选择D. 说明:如果函数解析式中的系数为固定值.可直接根据该函数的性质进行判断.
网址:http://m.1010jiajiao.com/timu3_id_486537[举报]
已知:反比例函数y=
(k≠0)经过点B(1,1).
(1)求该反比例函数解析式;
(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m,
m-1)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是
,求代数式n2+
n-2
的值.
查看习题详情和答案>>
| k |
| x |
(1)求该反比例函数解析式;
(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m,
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
已知:反比例函数y=-
.
(1)若将反比例函数y=-
的图象绕原点O旋转90°,求所得到的双曲线C的解析式并画图;
(2)双曲线C上是否存在到原点O距离为
的点P?若存在,求出点P的坐标.
查看习题详情和答案>>
| 6 |
| x |
(1)若将反比例函数y=-
| 6 |
| x |
(2)双曲线C上是否存在到原点O距离为
| 13 |
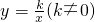 经过点B(1,1).
经过点B(1,1). )(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是
)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是 ,求代数式
,求代数式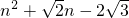 的值.
的值. 经过点B(1,1).
经过点B(1,1). )(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是
)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是 ,求代数式
,求代数式 的值.
的值.