摘要:2.理解平行四边形的概念,由平行四边形是中心对称图形探索它的性质.掌握平行四边形的性质定理.
网址:http://m.1010jiajiao.com/timu3_id_485188[举报]
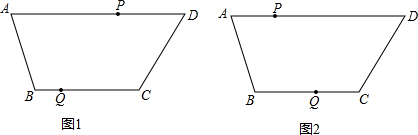
如图,在梯形ABCD中,AD∥BC,且AD>BC,BC=6cm,AD=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,其中一个动点到达终点时,另一个动点也停止运动.试计算,
(1)当运动时间为多少时,直线PQ四边形截出四边形是一个平行四边形?
(2)在直线PQ所截出的平行四边形中,在PQ的对边任取一点O,连接OP、OQ,得到△OPQ,则△OPQ的面积与直线PQ所截出的平行四边形的面积有何关系?并说明理由.(在图1、图2中任取一种画出图形,说明理由即可.)
查看习题详情和答案>>
(1)当运动时间为多少时,直线PQ四边形截出四边形是一个平行四边形?
(2)在直线PQ所截出的平行四边形中,在PQ的对边任取一点O,连接OP、OQ,得到△OPQ,则△OPQ的面积与直线PQ所截出的平行四边形的面积有何关系?并说明理由.(在图1、图2中任取一种画出图形,说明理由即可.)

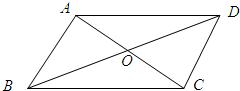 22、已知:四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:
22、已知:四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥DC;②OA=OC;③AB=DC;④∠BAD=∠DCB;⑤AD∥BC.
(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示):如①与⑤、
①与②、①与③
;(直接在横线上再写出两种)(2)对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举出反例说明.
以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
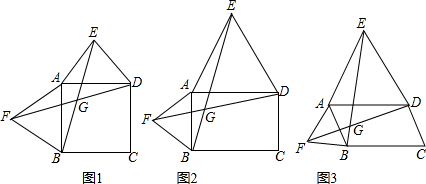
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看习题详情和答案>>

(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是
EB=FD
EB=FD
;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
如图,在一个平行四边形的活动框架上,用两根橡皮筋套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状,设这个平行四边形的一个内角为∠α.

(1)当∠α为多少度时,平行四边形变成矩形?
(2)由矩形的两条对角线相等且互相平分,可以得出“直角三角形斜边上的中线与斜边有怎样的数量关系”?
(3)矩形是轴对称图形吗?若是,它有几条对称轴?
(4)矩形是中心对称图形吗?若是,它的对称中心在何处? 查看习题详情和答案>>

(1)当∠α为多少度时,平行四边形变成矩形?
(2)由矩形的两条对角线相等且互相平分,可以得出“直角三角形斜边上的中线与斜边有怎样的数量关系”?
(3)矩形是轴对称图形吗?若是,它有几条对称轴?
(4)矩形是中心对称图形吗?若是,它的对称中心在何处? 查看习题详情和答案>>
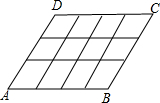 如图所示,一形状为平行四边形的草坪由12块相同的菱形草皮拼成,每块草皮的周长为4米,菱形的较小内角为60°,则这块草坪的面积为( )
如图所示,一形状为平行四边形的草坪由12块相同的菱形草皮拼成,每块草皮的周长为4米,菱形的较小内角为60°,则这块草坪的面积为( )| A、12m2 | ||
| B、16m2 | ||
C、6
| ||
D、3
|