题目内容
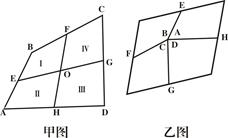
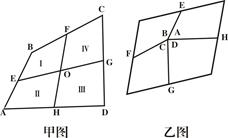
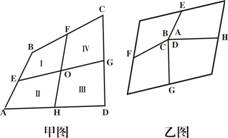
如图,在一个平行四边形的活动框架上,用两根橡皮筋套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状,设这个平行四边形的一个内角为∠α.
(1)当∠α为多少度时,平行四边形变成矩形?
(2)由矩形的两条对角线相等且互相平分,可以得出“直角三角形斜边上的中线与斜边有怎样的数量关系”?
(3)矩形是轴对称图形吗?若是,它有几条对称轴?
(4)矩形是中心对称图形吗?若是,它的对称中心在何处?
分析:(1)根据矩形的判定方法:一个内角是直角的平行四边形是矩形,可得答案;
(2)根据矩形的性质:对角线互相平分且相等可判断;
(3)根据轴对称图形的定义:沿一条直线对折后,直线两旁部分完全重合的图形是轴对称图形,即可判断出.
(4)根据中心对称图形的定义:旋转180°后能够与原图形完全重合即是中心对称图形,即可判断出.
(2)根据矩形的性质:对角线互相平分且相等可判断;
(3)根据轴对称图形的定义:沿一条直线对折后,直线两旁部分完全重合的图形是轴对称图形,即可判断出.
(4)根据中心对称图形的定义:旋转180°后能够与原图形完全重合即是中心对称图形,即可判断出.
解答: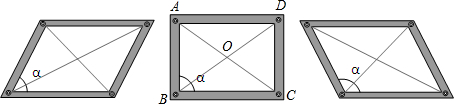
解:(1)当∠α=90°时,平行四边形变成矩形.
(2)可以,
∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∴BO=
AC,
即:直角三角形斜边上的中线等于斜边的一半.
(3)矩形是轴对称图形,它有2条对称轴.
(4)矩形是中心对称图形,它的对称中心是两条对角线的交点.

解:(1)当∠α=90°时,平行四边形变成矩形.
(2)可以,
∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∴BO=
| 1 |
| 2 |
即:直角三角形斜边上的中线等于斜边的一半.
(3)矩形是轴对称图形,它有2条对称轴.
(4)矩形是中心对称图形,它的对称中心是两条对角线的交点.
点评:此题主要考查了矩形的性质与判定,轴对称图形的定义,中心对称图形的定义,此题是一个综合题,难度不大,需要同学们牢固掌握基础知识.

练习册系列答案
相关题目
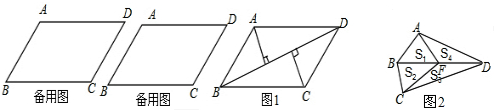
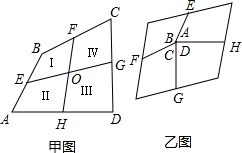 四块,然后再拼成一个平行四边形?
四块,然后再拼成一个平行四边形?