摘要:3.理解比和百分比的有关概念,会解决有关比和百分比的简单问题.在分数的应用中.体会数学与现实生活的联系(可涉及如合格率.增长率.利率.税率等术语)
网址:http://m.1010jiajiao.com/timu3_id_485114[举报]
作一个图形关于一条直线的轴对称图形,再将这个轴对称图形沿着与这条直线平行的方向平移,我们把这样的图形变换叫做关于这条直线的滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1),结合轴对称和平移的有关性质,解答以下问题: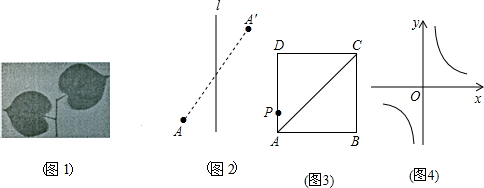
(1)如图2,在关于直线l的滑动对称变换中,试证明:两个对应点A,A′的连线被直线l平分;
(2)若点P是正方形ABCD的边AD上的一点,点P关于对角线AC滑动对称变换的对应点P′也在正方形ABCD的边上,请仅用无刻度的直尺在图3中画出P′;
(3)定义:若点M到某条直线的距离为d,将这个点关于这条直线的对称点N沿着与这条直线平行的方向平移到点M′的距离为s,称[d,s]为点M与M′关于这条直线滑动对称变换的特征量.如图4,在平面直角坐标系xOy中,点B是反比例函数y=
的图象在第一象限内的一个动点,点B关于y轴的对称点为C,将点C沿平行于y轴的方向向下平移到点B′.
①若点B(1,3)与B′关于y轴的滑动对称变换的特征量为[m,m+4],判断点B′是否在此函数的图象上,为什么?
②已知点B与B′关于y轴的滑动对称变换的特征量为[d,s],且不论点B如何运动,点B′也都在此函数的图象上,判断s与d是否存在函数关系?如果是,请写出s关于d的函数关系式. 查看习题详情和答案>>

(1)如图2,在关于直线l的滑动对称变换中,试证明:两个对应点A,A′的连线被直线l平分;
(2)若点P是正方形ABCD的边AD上的一点,点P关于对角线AC滑动对称变换的对应点P′也在正方形ABCD的边上,请仅用无刻度的直尺在图3中画出P′;
(3)定义:若点M到某条直线的距离为d,将这个点关于这条直线的对称点N沿着与这条直线平行的方向平移到点M′的距离为s,称[d,s]为点M与M′关于这条直线滑动对称变换的特征量.如图4,在平面直角坐标系xOy中,点B是反比例函数y=
| 3 | x |
①若点B(1,3)与B′关于y轴的滑动对称变换的特征量为[m,m+4],判断点B′是否在此函数的图象上,为什么?
②已知点B与B′关于y轴的滑动对称变换的特征量为[d,s],且不论点B如何运动,点B′也都在此函数的图象上,判断s与d是否存在函数关系?如果是,请写出s关于d的函数关系式. 查看习题详情和答案>>
圆的有关概念:
(1)圆两种定义方式:
(a)在一个平面内线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做
(b)圆是所有点到定点O的距离
(2)弦:连接圆上任意两点的
(3)弧:圆上任意两点间的部分叫
(4)等弧:在同圆与等圆中,能够
(5)等圆:能够
查看习题详情和答案>>
(1)圆两种定义方式:
(a)在一个平面内线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做
圆心
圆心
.线段OA叫做半径
半径
.(b)圆是所有点到定点O的距离
等于
等于
定长r的点的集合.(2)弦:连接圆上任意两点的
线段
线段
叫做弦.(弦不一定是直径,直径一定是弦,直径是圆中最长的弦);(3)弧:圆上任意两点间的部分叫
弧
弧
(弧的度数等于这条弧所对的圆心角的度数,等于这条弧所对圆周角的两倍)(4)等弧:在同圆与等圆中,能够
完全重合
完全重合
的弧叫等弧.(5)等圆:能够
完全重合
完全重合
的两个圆叫等圆,半径相等
相等
的两个圆也叫等圆..
党的十七大报告指出:要坚持和完善按劳分配为主体,多种分配方式并存的分配制度,健全劳动、资本、技术、管理等生产要素按贡献参与分配的制度,初次分配和再分配都要处理好效率和公平的关系,再分配要更加注重公平。逐步提高居民收入在国民收入分配中的比重,提高劳动报酬在初次分配中的比重。着力提高低收入者收入,逐步提高扶贫标准和最低工资标准,建立企业职工工资正常增长机制和支付保障机制。
试用经济生活知识回答:应怎样理解效率和公平的关系?(10分) 查看习题详情和答案>>
试用经济生活知识回答:应怎样理解效率和公平的关系?(10分) 查看习题详情和答案>>