Question

作一个图形关于一条直线的轴对称图形，再将这个轴对称图形沿着与这条直线平行的方向平移，我们把这样的图形变换叫做关于这条直线的滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换（如图1），结合轴对称和平移的有关性质，解答以下问题：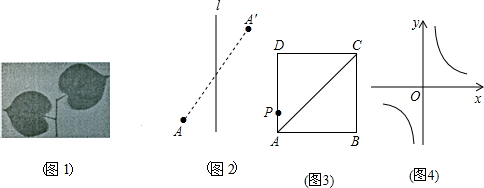
（1）如图2，在关于直线l的滑动对称变换中，试证明：两个对应点A，A′的连线被直线l平分；
（2）若点P是正方形ABCD的边AD上的一点，点P关于对角线AC滑动对称变换的对应点P′也在正方形ABCD的边上，请仅用无刻度的直尺在图3中画出P′；
（3）定义：若点M到某条直线的距离为d，将这个点关于这条直线的对称点N沿着与这条直线平行的方向平移到点M′的距离为s，称[d，s]为点M与M′关于这条直线滑动对称变换的特征量．如图4，在平面直角坐标系xOy中，点B是反比例函数y=

3

x

的图象在第一象限内的一个动点，点B关于y轴的对称点为C，将点C沿平行于y轴的方向向下平移到点B′．
①若点B（1，3）与B′关于y轴的滑动对称变换的特征量为[m，m+4]，判断点B′是否在此函数的图象上，为什么？
②已知点B与B′关于y轴的滑动对称变换的特征量为[d，s]，且不论点B如何运动，点B′也都在此函数的图象上，判断s与d是否存在函数关系？如果是，请写出s关于d的函数关系式．

Answer 1

分析：（1）作A关于直线l的对称点A′，根据相似三角形的性质和判定求出即可；
（2）连接BD交AC于O，作直线PO．即可得出答案；
（3）①根据已知求出b′的坐标，代入函数解析式看看两边是否相等即可；②作B关于y轴的对称点C，求出C的坐标，再根据平移规律得出即可．

解答：解：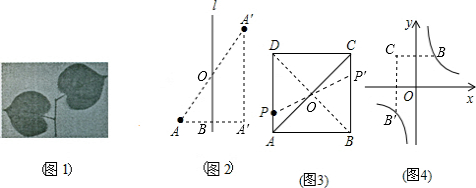
（1）如图1，作点A关于直线l的对称点A″，连接A′A″，
∵由题意知：A′A″∥直线l，
∴△AA′A″∽△ABO，
∵点B是AA″的中点，
∴

AO

AA′

=

AB

AA″

=

1

2

，
∴O为AA′的中点；

（2）连接BD交AC于O，连接PO并延长交BD于P′，则P′为所求；

（3）①点B′不在双曲线上，
理由是：∵点B（1，3）与B′关于y轴的滑动对称变换的特征量为[m，m+4]，
∴m=1，m+4=5，
∴B′的坐标是（-1，-2），
把B′的坐标代入双曲线y=

3

x

，左右两边不相等，
∴点B′不在双曲线上；
②s与d存在函数关系，
如图3，作B关于直线y的对称点C，连接B′C，
点B与B'关于y轴的滑动对称变换特征量为[d，s]
设点B的坐标为（d，

3

d

），则点C的坐标为（-d，

3

d

）
∴点B'的坐标为（-d，

3

d

-s），
又∵点B'在函数y=

3

x

图象上，
∴-d×(

3

d

-s)=3，
得d•s=6，则s=

6

d

．

点评：本题考查了双曲线的性质，正方形的性质，轴对称性质的应用，主要考查学生的阅读理解能力和计算能力，题目是一道比较典型的题目，比较好．