摘要：13．如图.沿长方形ABCD的对角线BD与长方形A1B1C1D1的对角线B1D1将长方体截成相等的两部分.截面BDD1B1.是一个 形.与它平行的棱有 .
网址：http://m.1010jiajiao.com/timu3_id_484562[举报]
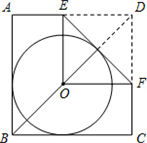
如图.O是正方形 ABCD的对角线BD 上一点，⊙O与边AB，BC都相切，点E，F分别在边AD，DC上. 现将△DE.F沿着EF 对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处. 若DE=2. 则正方形ABCD 的边长是
[ ]
A.3
B.4
C.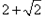
D.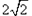
查看习题详情和答案>>
B.4
C.
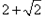
D.
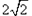
如图，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．
(1)求证：
；
(2)点C1从点C出发，沿着线段CB向点B运动(不与点B重合)，同时点A1从点A出发，沿着BA的延长线运动，点C1与A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动．如图，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想E1F1，
与AB三者之间的数量关系，并证明你的猜想；
(3)在(2)的条件下，当A1E1＝3，C1E1＝2时，求BD的长．
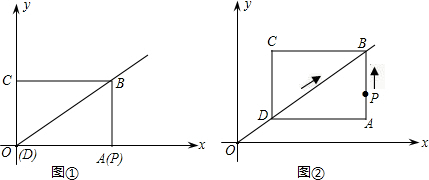
如图，正方形ABCD的边长为5cm，动点P从点C出发，沿折线C-B-A-D向终点D运动，速度为acm/s；动点Q从点B出发，沿对角线BD向终点D运动，速度为
cm/s．当其中一点到达自己的终点时，另一点也停止运动．当点P、点Q同时从各自的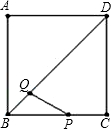
起点运动时，以PQ为直径的⊙O与直线BD的位置关系也随之变化，设运动时间为t（s）．
（1）写出在运动过程中，⊙O与直线BD所有可能的位置关系 ；
（2）在运动过程中，若a=3，求⊙O与直线BD相切时t的值；
（3）探究：在整个运动过程中，是否存在正整数a，使得⊙O与直线BD相切两次？若存在，请直接写出符合条件的两个正整数a及相应的t的值；若不存在，请说明理由． 查看习题详情和答案>>
| 2 |
起点运动时，以PQ为直径的⊙O与直线BD的位置关系也随之变化，设运动时间为t（s）．（1）写出在运动过程中，⊙O与直线BD所有可能的位置关系
（2）在运动过程中，若a=3，求⊙O与直线BD相切时t的值；
（3）探究：在整个运动过程中，是否存在正整数a，使得⊙O与直线BD相切两次？若存在，请直接写出符合条件的两个正整数a及相应的t的值；若不存在，请说明理由． 查看习题详情和答案>>
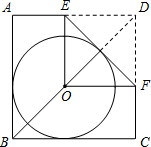如图，O是正方形ABCD的对角线BD上一点，⊙O与边AB，BC都相切，点E，F分别在AD，DC上，现将△DEF沿着EF对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处．若DE=2，则正方形ABCD的边长是（ ）