摘要： 如图6.在正方形ABCD中.G是BC上的任意一点..E.F是AG上的两点.若AF=BF+EF.∠1=∠2.请判断线段DE与BF有怎样的位置关系.并证明你的结论. 解:根据题目条件可判断DE//BF. 证明如下: ∵四边形ABCD是正方形. ∴AB=AD.∠BAF+∠2=90°. ∵AF=AE+EF.又AF=BF+EF ∴AE=BF ∵∠1=∠2.∴△ABF≌△DAE(SAS). ∴∠AFB=∠DEA.∠BAF=∠ADE. ∴∠ADE+∠2=90°. ∴∠AED=∠BFA=90°. ∴DE//BF.
网址：http://m.1010jiajiao.com/timu3_id_482208[举报]
（本小题满分8分）如图1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图2的程序移动．
1.（1）请在图1中画出光点P经过的路径；
2.（2）求光点P经过的路径总长（结果保留π）．
查看习题详情和答案>>
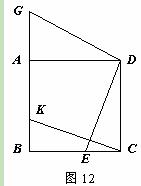
（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB
上，点G在BA的延长线上，且CE=BK=AG.
⑴求证：①DE=DG；②DE⊥DG；
⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；
⑷当
时，请直接写出
的值.
查看习题详情和答案>>
（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB
上，点G在BA的延长线上，且CE=BK=AG.
⑴求证：①DE=DG；②DE⊥DG；
⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；
⑷当
时，请直接写出
的值.
查看习题详情和答案>>
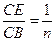时，请直接写出
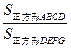的值.