摘要:2.图形的平移:通过具体实例认识平移.理解对应点连线平行且相等的性质, 能按要求作出简单平面图形平移后的图形,利用平移进行图案设计.认识和欣赏平移在现实生活中的应用.
网址:http://m.1010jiajiao.com/timu3_id_479986[举报]
数学活动与思考
我们要学会用数学的眼光看世界--丰富多彩的图形世界.在“图形世界”里,见到许多熟悉的基本图形,感受到图形的平移、翻折、旋转等变化;也发现“图形世界”是由基本图形构成的.可以利用这些变化和基本图形设计出符合要求的图形.
例:直角三角形通过剪切可以拼成一个与该直角三角形面积相等的长方形.方法如图示:
请你用图示的方法解答下列问题:

(1)如图,对一个任意的三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的长方形;

(2)如图,对一个任意的四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的长方形;
查看习题详情和答案>>
我们要学会用数学的眼光看世界--丰富多彩的图形世界.在“图形世界”里,见到许多熟悉的基本图形,感受到图形的平移、翻折、旋转等变化;也发现“图形世界”是由基本图形构成的.可以利用这些变化和基本图形设计出符合要求的图形.
例:直角三角形通过剪切可以拼成一个与该直角三角形面积相等的长方形.方法如图示:
请你用图示的方法解答下列问题:

(1)如图,对一个任意的三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的长方形;

(2)如图,对一个任意的四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的长方形;

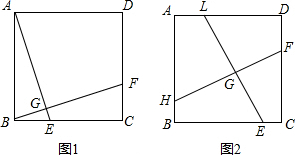
27、如图1,点E、F在正方形ABCD的边BC、CD上,且AE⊥BF于G.


(1)AE与BF相等吗?请说明理由;
(2)运用图形的平移、旋转方法,分析说明△ABE和△BCF可以通过怎样的平移和旋转而相互得到如图1,点H、E、F、L在正方形ABCD的边上,且LE⊥HF于G,图2通过怎样的方法可以得到图1,从而分析说明LE与HF相等.
查看习题详情和答案>>


(1)AE与BF相等吗?请说明理由;
(2)运用图形的平移、旋转方法,分析说明△ABE和△BCF可以通过怎样的平移和旋转而相互得到如图1,点H、E、F、L在正方形ABCD的边上,且LE⊥HF于G,图2通过怎样的方法可以得到图1,从而分析说明LE与HF相等.
(2013•六合区一模)我们可以将一个纸片通过剪切,结合图形的平移、旋转、翻折,重新拼接成一个新的图形.如图1,沿△ABC的中位线DE剪切,将△ADE绕点E顺时针旋转180°,可得到?BCFD.请尝试解决下面问题(写画法,保留痕迹,并作必要说明):
(1)将梯形纸片剪拼成平行四边形:请在图2中画出示意图,要求用两种不同的画法,并简要说明如何剪拼和变换的;

(2)如图3,将四边形ABCD剪拼成平行四边形.在图中画出示意图.
查看习题详情和答案>>
(1)将梯形纸片剪拼成平行四边形:请在图2中画出示意图,要求用两种不同的画法,并简要说明如何剪拼和变换的;

(2)如图3,将四边形ABCD剪拼成平行四边形.在图中画出示意图.
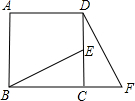 如图,在正方形ABCD中,E是CD的中点,F是BC延长线上的一点,CF=
如图,在正方形ABCD中,E是CD的中点,F是BC延长线上的一点,CF=