摘要：26． 解:(1)过E点作EF∥AB交CN于F. 由△CEF-△CAN知: 2EF=AN - 1分- 又由 知△EFM≌△DNM(ASA) 所以EF=DN - 2分- 所以AN=2DN - 3分- 设△DNM DM边上的高为h.则△ADE DE边上的高为3h DM=ME=x 则 故 - 4分- (2)由于该同学设计制作均属同一材料.且厚度不计 故等腰梯形ABCD的面积与(1)中△ABC的面积相等 则: 故 - 5分- 设等腰梯形ABCD中AD=x 则BC=4-x 由△HEG-△HBC 设EG边上的高为 则 - 6分- - 7分- - 8分- 故当时.的比值最大.为 即当时.的比值最大.为 - 9分- (3)过E点作EI∥AB交NG于I.过C点作CQ∥AB交NG延长线于Q. 设BC=2.ND=x 由得: IE=ND 又△DCG-△IEM 知 - 10分- 又由梯形中位线性质: 故 - 11分- 故时. 为函数的对称轴. 故时.函数单调递减.故此时 - 12分- 故存在.此时. - 13分- 2005年厦门质检
网址：http://m.1010jiajiao.com/timu3_id_479097[举报]
30、阅读理解，填写部分理由，探索新的结论（②③两小题只写结论）
已知AB∥CD，①如图，∠B+∠C=∠BEC．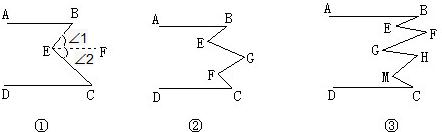
理由如下：
解：过E点作EF∥AB
则∠1=∠B（
∵EF∥AB
AB∥CD（
∴EF∥CD（
∴∠2=∠C（
∵∠BEC=∠1+∠2
∴∠BEC=∠C+∠B（
②图乙中∠B，∠E，∠D，∠F，∠C的数量关系是
③图丙中∠B，∠E，∠F，∠G，∠H，∠M，∠C的数量关系是
查看习题详情和答案>>
已知AB∥CD，①如图，∠B+∠C=∠BEC．
理由如下：
解：过E点作EF∥AB
则∠1=∠B（
两直线平行内错角相等
）∵EF∥AB
AB∥CD（
已知
）∴EF∥CD（
如果两条直线都与第三条直线平行，那么这两条直线也互相平行
）∴∠2=∠C（
两直线平行内错角相等
）∵∠BEC=∠1+∠2
∴∠BEC=∠C+∠B（
等量代换
）②图乙中∠B，∠E，∠D，∠F，∠C的数量关系是
∠B+∠G+∠C=∠E+∠F
；③图丙中∠B，∠E，∠F，∠G，∠H，∠M，∠C的数量关系是
∠B+∠F+∠H+∠C=∠E+∠G+∠M
．阅读理解，填写部分理由，探索新的结论（②③两小题只写结论）
已知AB∥CD，①如图，∠B+∠C=∠BEC．
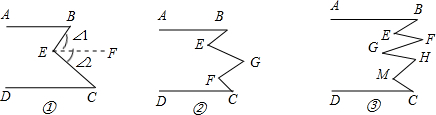
理由如下：
解：过E点作EF∥AB
则∠1=∠B（________）
∵EF∥AB
AB∥CD（________）
∴EF∥CD（________）
∴∠2=∠C（________）
∵∠BEC=∠1+∠2
∴∠BEC=∠C+∠B（________）
②图乙中∠B，∠E，∠D，∠F，∠C的数量关系是________；
③图丙中∠B，∠E，∠F，∠G，∠H，∠M，∠C的数量关系是________．
查看习题详情和答案>>
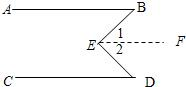18、如图，已知AB∥CD，求证：∠B+∠D=∠BED，试完成下列的证明过程．证明：过E点作EF∥AB（已作）
∴∠1=∠B （
两直线平行，内错角相等
）又∵AB∥CD （
已知
）∴EF∥CD （
平行的传递性
）∴
∠2=∠D
∴∠B+∠D=∠1+∠2
∴∠BED=∠B+∠D （
等量代换
）
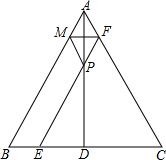如图，在等腰△ABC中，AB=AC，AD是∠BAC的角平分线，P是AD上任意一点，过P点作EF∥AB，PM∥AC．
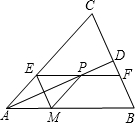EF∥AB，分别交AC，BC于E，F点，作PM∥AC，交AB于M点，连接ME．