摘要:25.(1)证明:∵AB为圆O1之直径 ∴∠ADB=90°. 又∠ADB与∠ADC互补 ∴∠ADC=90°. ∴AC是⊙O2的直径; (2)证明:连结O1O2. ∵=且∠BAC=∠O1A O2 ∴△AO1O2∽△ABC 又O1A= O1O2 ∴AB=BC (3)解:设AG=x ∵A O2= O2C且AB=BC ∴AB=BC=4 而∠DAC=∠O2BC.∠A O2B=∠B O2C. ∴△AGO2∽△BCO2 ∴= .解得:x=
网址:http://m.1010jiajiao.com/timu3_id_479078[举报]
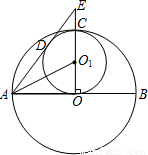
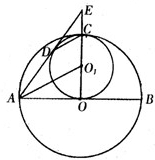 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.
如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.(1)试探究CD与AO1的位置关系,并说明理由;
(2)若DE=4,CE=2,求AD的长.
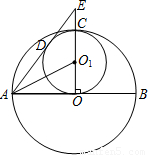
 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1=
如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1=