摘要:[答案](1)解法一:∵抛物线=-++经过点A. ∴=-4 又由题意可知..是方程-++=0的两个根. ∴+=. =-=6 由已知得(-)=25 又(-)=(+)-4=-24 ∴ -24=25 .解得=± 当=时.抛物线与轴的交点在轴的正半轴上.不合题意.舍去. ∴=-. 解法二:∵.是方程-++c=0的两个根. 即方程2-3+12=0的两个根. ∴=. ∴-==5. 解得 =± (2)∵四边形BDCE是以BC为对角线的菱形.根据菱形的性质.点D必在抛物线的对称轴上. 又∵=---4=-(+)+ ∴抛物线的顶点(-.)即为所求的点D. (3)∵四边形BPOH是以OB为对角线的菱形.点B的坐标为. 根据菱形的性质.点P必是直线=-3与 抛物线=---4的交点. ∴当=-3时.=-×(-3)-×(-3)-4=4. ∴在抛物线上存在一点P.使得四边形BPOH为菱形. 四边形BPOH不能成为正方形.因为如果四边形BPOH为正方形.点P的坐标只能是.但这一点不在抛物线上.
网址:http://m.1010jiajiao.com/timu3_id_478907[举报]
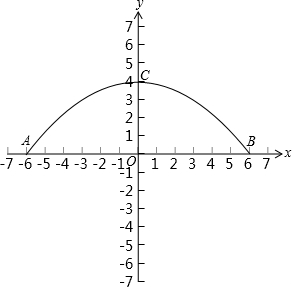
如图,河上有一座抛物线形状的桥洞,已知桥下的水面离桥拱顶部4米时,水面宽AB为12米,如图建立直角坐标系.
(1)求抛物线的函数解析式;
(2)当水位上升1米时,水面宽为多少米?(答案保留整数,其中
≈1.7)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求抛物线的函数解析式;
(2)当水位上升1米时,水面宽为多少米?(答案保留整数,其中
| 3 |
 查看习题详情和答案>>
查看习题详情和答案>>
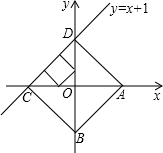
如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
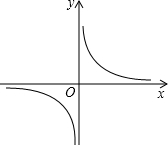
(2)若某函数是反比例函数y=
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
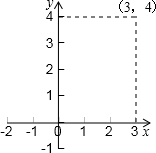
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 ,写出符合题意的其中一条抛物线解析式 ,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数? .(本小题只需直接写出答案)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;

(2)若某函数是反比例函数y=
| k | x |

(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标
 查看习题详情和答案>>
查看习题详情和答案>>
 在8×8的网格图中建立如图坐标系,每个小正方形的顶点称为格点.在网格图中画一条抛物线经过81个格点中的8个格点,则该抛物线的解析式为
在8×8的网格图中建立如图坐标系,每个小正方形的顶点称为格点.在网格图中画一条抛物线经过81个格点中的8个格点,则该抛物线的解析式为