题目内容
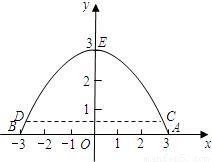
如图,河上有一座抛物线形状的桥洞,已知桥下的水面离桥拱顶部4米时,水面宽AB为12米,如图建立直角坐标系.(1)求抛物线的函数解析式;
(2)当水位上升1米时,水面宽为多少米?(答案保留整数,其中
| 3 |
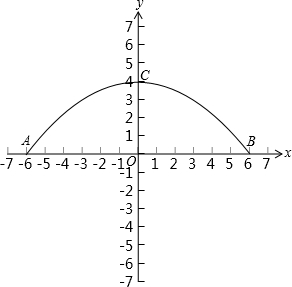
分析:(1)根据抛物线在坐标系的位置及顶点坐标设顶点式,将B(6,0)代入解析式求a即可确定函数解析式;
(2)水位上升1米,即y=1,代入函数式求x的值,根据抛物线的对称性求水面宽.
(2)水位上升1米,即y=1,代入函数式求x的值,根据抛物线的对称性求水面宽.
解答:解:(1)设函数解析式为y=ax2+4,
将B(6,0)代入解析式y=ax2+4,
解得a=-
,
∴抛物线的函数解析式为y=-
x2+4.
(2)当y=1时,1=-
×x2+4,
解得x=3
,2x=6
≈10.
当水位上1米时,水面宽约为10米.
将B(6,0)代入解析式y=ax2+4,
解得a=-
| 1 |
| 9 |
∴抛物线的函数解析式为y=-
| 1 |
| 9 |
(2)当y=1时,1=-
| 1 |
| 9 |
解得x=3
| 3 |
| 3 |
当水位上1米时,水面宽约为10米.
点评:本题考查了根据抛物线在坐标系的位置,适当设抛物线解析式的方法,以及二次函数的实际运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
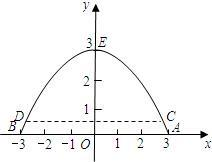 度是多少米?
度是多少米? m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?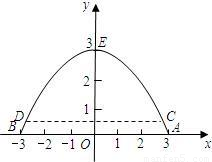
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?