摘要：[答案] Ⅰ.证明:∵DEFG为正方形.∴GD=FE.∠GDB=∠FEC=90° ∵△ABC是等边三角形.∴∠B=∠C=60° ∴△BDG≌△CEF(AAS) Ⅱa.解法一:设正方形的边长为x.作△ABC的高AH. 求得.由△AGF∽△ABC得: 解之得:(或) 解法二:设正方形的边长为x.则 在Rt△BDG中.tan∠B=. ∴ 解之得:(或) 解法三:设正方形的边长为x.则 由勾股定理得: 解之得: Ⅱb.解: 正确 由已知可知.四边形GDEF为矩形 ∵FE∥F’E’ . ∴.同理.∴ 又∵F’E’=F’G’. ∴FE=FG 因此.矩形GDEF为正方形
网址：http://m.1010jiajiao.com/timu3_id_478905[举报]
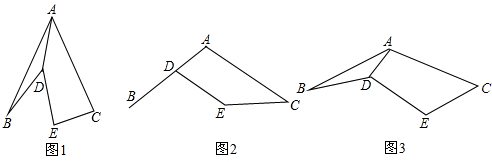
已知AB=AC，DB=DE，∠BAC=∠BDE=α．
（1）若α=60°（如图1）探究线段AD与CE的数量关系，并加以证明；
（2）若α=120°，并且点D在线段AB上，（如图2）则线段AD与CE的数量关系为 ；（直接写出答案）
（3）探究线段AD与CE的数量关系（如图3）并加以证明．
查看习题详情和答案>>
（1）若α=60°（如图1）探究线段AD与CE的数量关系，并加以证明；
（2）若α=120°，并且点D在线段AB上，（如图2）则线段AD与CE的数量关系为
（3）探究线段AD与CE的数量关系（如图3）并加以证明．
查看习题详情和答案>>
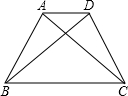如图，已知在等腰梯形ABCD中，AD∥BC．（1）若AD=5，BC=11，梯形的高是4，求梯形的周长；
（2）若AD=a，BC=b，梯形的高是h，梯形的周长为c．则c=
（请用含a、b、h的代数式表示；答案直接写在横线上，不要求证明．）
（3）若AD=3，BC=7，BD=5
| 2 |
如图，已知：AB=AC，直线m经过点A，点D、E是直线m上两个动点，连接BD、CE．
（1）如图1，若∠BAC=90°，BD⊥DE，CE⊥DE．求证：DE=BD+CE．
（2）如图2，若∠BAC=∠BDA=∠AEC，则（1）中的结论DE=BD+CE还成立吗？（只回答答案，不用证明）
（3）如图3，在（2）的条件下，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，是判定△DEF的形状，并证明你的判定．
查看习题详情和答案>>
（1）如图1，若∠BAC=90°，BD⊥DE，CE⊥DE．求证：DE=BD+CE．
（2）如图2，若∠BAC=∠BDA=∠AEC，则（1）中的结论DE=BD+CE还成立吗？（只回答答案，不用证明）
（3）如图3，在（2）的条件下，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，是判定△DEF的形状，并证明你的判定．
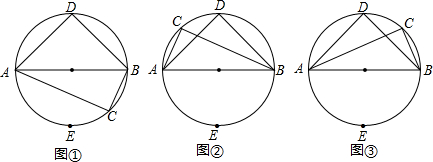
（2013•尤溪县质检）如图①，在⊙O中AB是直径，D是上半圆中点，E是下半圆中点，点C是⊙O上一点（不与B、E重合）连接AD、BD、AC、BC．设BC长度为n，AC长度为m．
（1）用含m、n的式子表示四边形ACBD的面积S；
（2）证明：tan∠DAC=
；
（3）如图②③，当点C运动至
或
上时，②中结论是否成立？若成立，请说明理由；若不成立，请用含m、n的式子表示tan∠DAC．（直接写答案，并选择其中一种证明）
查看习题详情和答案>>
（1）用含m、n的式子表示四边形ACBD的面积S；
（2）证明：tan∠DAC=
| m+n |
| m-n |
（3）如图②③，当点C运动至
 |
| AD |
|
| BD |
阅读下列材料，解答相应问题：
已知△ABC是等边三角形，AD是高，设AD=h．点P（不与点A、B、C重合）到AB的距离PE=h1，到AC的距离PF=h2，到BC的距离PH=h3．
如图1，当点P与点D重合时，我们容易发现：h1=
h，h2=
h，因此得到：h1+h2=h．
小明同学大胆猜想提出问题：如图2，若点P在BC边上，但不与点D重合，结论h1+h2=h还成立吗？通过证明，他得到了肯定的答案．证明如下：
证明：如图3，连接AP．
∴S△ABC=S△ABP+S△APC．
设等边三角形的边长AB=BC=CA=a．
∵AD⊥BC，PE⊥AB，PF⊥AC，
∴
BC•AD=
AB•PE+
AC•PF
∴
a•h=
a•h1+
a•h2．
∴h1+h2=h．
（1）进一步猜想：当点P在BC的延长线上，上述结论还成立吗？若成立，请你证明；若不成立，请猜想h1，h2与 h之间的数量关系，并证明．（借助答题卡上的图4）
（2）我们容易知道，当点P在CB的延长线及直线AB，AC上时，情况与前述类似，这里不再说明．
继续猜想，你会进一步提出怎样的问题呢？请在答题卡上借助图5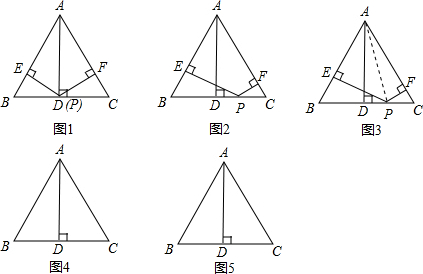
画出示意图，写出你提出的问题，并直接写出结论，不必证明．
查看习题详情和答案>>
已知△ABC是等边三角形，AD是高，设AD=h．点P（不与点A、B、C重合）到AB的距离PE=h1，到AC的距离PF=h2，到BC的距离PH=h3．
如图1，当点P与点D重合时，我们容易发现：h1=
| 1 |
| 2 |
| 1 |
| 2 |
小明同学大胆猜想提出问题：如图2，若点P在BC边上，但不与点D重合，结论h1+h2=h还成立吗？通过证明，他得到了肯定的答案．证明如下：
证明：如图3，连接AP．
∴S△ABC=S△ABP+S△APC．
设等边三角形的边长AB=BC=CA=a．
∵AD⊥BC，PE⊥AB，PF⊥AC，
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h1+h2=h．
（1）进一步猜想：当点P在BC的延长线上，上述结论还成立吗？若成立，请你证明；若不成立，请猜想h1，h2与 h之间的数量关系，并证明．（借助答题卡上的图4）
（2）我们容易知道，当点P在CB的延长线及直线AB，AC上时，情况与前述类似，这里不再说明．
继续猜想，你会进一步提出怎样的问题呢？请在答题卡上借助图5
画出示意图，写出你提出的问题，并直接写出结论，不必证明．
查看习题详情和答案>>