摘要:[解析]我们可以先假设存在这样的抛物线.如果能够求出对应的值.则存在.如果求不出.则不存在. [答案](1)∵ 平移的图象得到的抛物线F的顶点为Q, ∴ 抛物线对应的解析式为:. ∵ 抛物线与x轴有两个交点.∴. 令, 得., ∴ 即, 所以当时, 存在抛物线F使得. (2) ∵,∴ .得F: , 解得 在中, 1) 当时,由 , 得, 当时, 由, 解得, 此时, 二次函数解析式为; 当时, 由 ==, 解得, 此时.二次函数解析式为 + +. 2) 当时, 由 , 将代, 可得, , (也可由代.代得到) 所以二次函数解析式为 + –或.
网址:http://m.1010jiajiao.com/timu3_id_478894[举报]
你能求(x-1)(x99+x98+x97+…+x+1)的值吗
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x-1)(x+1)= ;
(2)(x-1)(x2+x+1)= ;
(3)(x-1)(x3+x2+x+1)= ;…
由此我们可以得到(x-1)(x99+x98+x97+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+…+2+1;
(2)(-2)50+(-2)49+(-2)48+…(-2)+1. 查看习题详情和答案>>
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x-1)(x+1)=
(2)(x-1)(x2+x+1)=
(3)(x-1)(x3+x2+x+1)=
由此我们可以得到(x-1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+…+2+1;
(2)(-2)50+(-2)49+(-2)48+…(-2)+1. 查看习题详情和答案>>
你能求(x-1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:①(x-1)(x+1)=x2-1;②(x-1)(x2+x+1)=x3-1;③(x-1)(x3+x2+x+1)=x4-1;…
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,完成下面的计算:
299+298+297+…+2+1.
查看习题详情和答案>>
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=
x100-1
x100-1
;请你利用上面的结论,完成下面的计算:
299+298+297+…+2+1.
阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题:1+2+3+…+100=?我们可以先从简单的几个数开始,计算、观察,寻求规律,得出一般性的结论.1=
=1,1+2=
=3,1+2+3=
=6,1+2+3+4=
=10;…,
(1)计算:1+2+3+…+100=
(2)计算:41+42+43+…+100=
查看习题详情和答案>>
| 1×2 |
| 2 |
| 2×3 |
| 2 |
| 3×4 |
| 2 |
| 4×5 |
| 2 |
(1)计算:1+2+3+…+100=
5050
5050
.(2)计算:41+42+43+…+100=
5050
5050
-820
820
=4230
4230
.
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?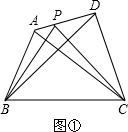
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=
AD时(如图②):
∵AP=
AD,△ABP和△ABD的高相等,
∴S△ABP=
S△ABD.
∵PD=AD-AP=
AD,△CDP和△CDA的高相等,
∴S△CDP=
S△CDA.
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-
S△ABD-
S△CDA
=S四边形ABCD-
(S四边形ABCD-S△DBC)-
(S四边形ABCD-S△ABC)
=
S△DBC+
S△ABC.
(2)当AP=
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(4)一般地,当AP=
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=
AD(0≤
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
查看习题详情和答案>>

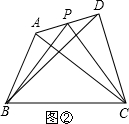
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=
| 1 |
| 2 |

∵AP=
| 1 |
| 2 |
∴S△ABP=
| 1 |
| 2 |
∵PD=AD-AP=
| 1 |
| 2 |
∴S△CDP=
| 1 |
| 2 |
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-
| 1 |
| 2 |
| 1 |
| 2 |
=S四边形ABCD-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当AP=
| 1 |
| 3 |
(3)当AP=
| 1 |
| 6 |
(4)一般地,当AP=
| 1 |
| n |
问题解决:当AP=
| m |
| n |
| m |
| n |