[解析]从函数图象容易看出前面一段是出台该项优惠政策前的情况.后面一段是出台该项优惠政策后的情况.前面一段所有的量已经知道.容易求出该果园共销售脐橙的重量.为后面一段的求值奠定了基础. [答案]解:——青夏教育精英家教网——

摘要：[解析]从函数图象容易看出前面一段是出台该项优惠政策前的情况.后面一段是出台该项优惠政策后的情况.前面一段所有的量已经知道.容易求出该果园共销售脐橙的重量.为后面一段的求值奠定了基础. [答案]解:(1)政策出台前的脐橙售价为 , (2)设剩余脐橙为x吨,则 103×x=11.7×104 ∴ 该果园共销售了10 +30 = 40吨脐橙 , (3)①设这个一次函数的解析式为. 代入两点得: 函数关系式为. ②令答:(1)原售价是3元/千克,(2)果园共销售40吨脐橙,(3)①函数关系式为, ②今年至少要销售35吨.总收入才达到去年水平．

网址：http://m.1010jiajiao.com/timu3_id_478891[举报]

如图是一种新型的滑梯的示意图，其中线段PA是高度为6米的平台，滑道AB是函数y=

的图象的一部分，滑道BCD是二次函数图象的一部分，两滑道的连接点B为抛物线的顶点，且B点到地面的距离为2米，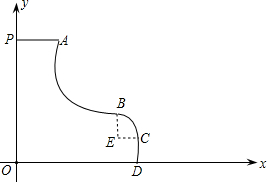

当甲同学滑到C点时，距地面的距离为1米，距点B的水平距离CE也为1米．
（1）试求滑道BCD所在抛物线的解析式．
（2）试求甲同学从点A滑到地面上D点时，所经过的水平距离．查看习题详情和答案>>

一慢车和一快车沿相同路线从A地到相距120千米的B地，所行地路程与时间的函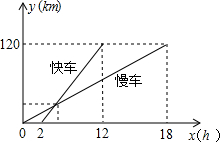

数图象如图所示．试根据图象，回答下列问题：
（1）慢车比快车早出发

小时，快车比慢车少用

小时到达B地；
（2）根据图象分别求出慢车和快车路程与时间的解析式．
（3）快车用了多少时间追上慢车；此时相距A地多少千米？查看习题详情和答案>>

小张骑车往返于甲、乙两地，他距甲地的路程y（千米）与时间x（小时）的函数图象如图中折线OABCD所示．
（1）小张在路上停留了

小时，他从乙地返回时的速度为

千米/小时；
（2）求小张在图中BC段上距甲地的路程y₁（千米）与时间x（小时）的函数解析式，并写出自变量x的取值范围；
（3）小王与小张同时从不同地点出发，按相同路线前往乙地，如果小王距甲地的路程y₂（千米）与时间x（小时）的函数关系式y₂=12x+10，图象为线段EF，那么他们第一次相遇时距出发多少小时？请写出你的计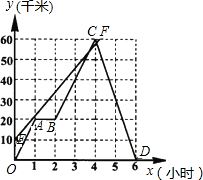

算过程．查看习题详情和答案>>

A、B两港相距240千米，甲、乙两艘货轮分别从A、B两港同时出发，相向而行．甲货轮顺流航行，乙货轮逆流航行，两艘货轮到达各自的目的地后均不在行驶．两艘货轮在静水中航行的速度相同．两艘货轮间的距离y（千米）与乙货轮行驶的时间x（小时）之间的函数图象如图所示：
（1）求两艘货轮的静水速度和水流速度；
（2）请说明图中N点的实际意义，并求线段NF的解析式，写出自变量x的取值范围；
（3）若在甲、乙两船出发的同时，还有一艘巡逻艇从A港出发（巡逻艇在静水中的速度是货轮静水中的速度的1.8倍）往返于A、B两港之间进行检查．当巡逻艇到达B港时，接到命令，要求巡逻艇马上返回追赶乙货轮，并对乙货轮进行进一步的检查，巡逻艇马上将其静水速度提高到原来的

倍，前去追赶乙货轮，问乙货轮出

发多长时间被巡逻艇追上（巡逻艇折返的时间忽略不计）？查看习题详情和答案>>

甲、乙两人同时从村庄沿一条路赴县城办事，甲开汽车，乙骑自行车，两人都匀速前进．甲先到县城，花了半小时办完事，然后按原路以另一速度匀速返回，直到与乙相遇，乙骑自行车的速度为20km/h．如图是两车之间的距离y（km）与乙行驶时间x（min）之间的函数图象，以下结论正确的有（　　）
（1）村庄与县城的距离为15km；
（2）甲开汽车去县城时的速度是80km/h；
（3）线段AB的解析式为y=-

x+20；
（4）甲开汽车返回时的速度是40km/h．

A．（2）（3）（4）

B．（1）（3）（4）

C．（1）（2）（4）

D．（1）（2）（3）

查看习题详情和答案>>