摘要：[答案]:(1)①CF与BD位置关系是 垂直.数量关系是相等, ②当点D在BC的延长线上时①的结论仍成立． 由正方形ADEF得 AD=AF .∠DAF=90º． ∵∠BAC=90º.∴∠DAF=∠BAC . ∴∠DAB=∠FAC. 又AB=AC .∴△DAB≌△FAC . ∴CF=BD ∠ACF=∠ABD． ∵∠BAC=90º. AB=AC .∴∠ABC=45º.∴∠ACF=45º. ∴∠BCF=∠ACB+∠ACF= 90º．即 CF⊥BD (2)画图正确 当∠BCA=45º时.CF⊥BD． 理由是:过点A作AG⊥AC交BC于点G.∴AC=AG 可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º ∠BCF=∠ACB+∠ACF= 90º． 即CF⊥BD (3)当具备∠BCA=45º时. 过点A作AQ⊥BC交BC的延长线于点Q. ∵DE与CF交于点P时. ∴此时点D位于线段CQ上. ∵∠BCA=45º.可求出AQ= CQ=4．设CD=x .∴ DQ=4-x. 容易说明△AQD∽△DCP.∴ . ∴.． ∵0＜x≤3 ∴当x=2时.CP有最大值1．
网址：http://m.1010jiajiao.com/timu3_id_478885[举报]
已知，在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边作正方形ADEF，连接CF．
（1）如图1，当点D在线段BC上时，求证：①CF=BD；②CF⊥BD．
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，线段CF与BD的上述关系是否还成立？请直接写出结论即可（不必证明）．
（3）如图3，当点D在线段BC的反向延长线上，且点A、F在直线BC的两侧，其它条件不变，线段CF与BD的上述关系是否还成立？若成立，请证明你的结论；若不成立，请说明理由．
查看习题详情和答案>>
（1）如图1，当点D在线段BC上时，求证：①CF=BD；②CF⊥BD．
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，线段CF与BD的上述关系是否还成立？请直接写出结论即可（不必证明）．
（3）如图3，当点D在线段BC的反向延长线上，且点A、F在直线BC的两侧，其它条件不变，线段CF与BD的上述关系是否还成立？若成立，请证明你的结论；若不成立，请说明理由．
如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为直角边且在AD的上方作等腰直角三角形ADF．
（1）若AB=AC，∠BAC=90°．
①当点D在线段BC上时（与点B不重合），试探讨CF与BD的数量关系和位置关系；
②当点D在线段BC的延长线上时，①中的结论是否仍然成立，请在图2中画出相应图形并说明理由；
（2）如图3，若AB≠AC，∠BAC≠90°，∠BCA=45°点D在线段BC上运动，试探究CF与BC位置关系．
查看习题详情和答案>>
（1）若AB=AC，∠BAC=90°．
①当点D在线段BC上时（与点B不重合），试探讨CF与BD的数量关系和位置关系；
②当点D在线段BC的延长线上时，①中的结论是否仍然成立，请在图2中画出相应图形并说明理由；
（2）如图3，若AB≠AC，∠BAC≠90°，∠BCA=45°点D在线段BC上运动，试探究CF与BC位置关系．
（2013•临汾二模）操作与证明
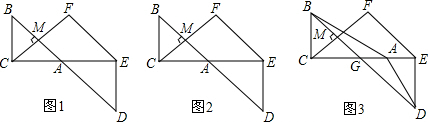
把两个全等的含45°角的三角板按如图所示的位置放置，使B、A、D在一条直线上，C、A、E在一条直线上，过点C作CM⊥BD于M，过点E作EF∥BD；直线CM与EF相交于点F．
（1）求证：△CEF是等腰直角三角形．
猜想与发现
（2）在图1的条件下，CF与BD的数量关系为
（3）如图2若把图1中Rt△ADE换为Rt△ABC不全等但相似的三角板时，其他条件不变，此时CF与BD的数量关系为
拓展与探究
（4）如图3若将图1中的两块三角板换成任意两个全等的直角三角形（Rt△ABC≌Rt△DAE），使锐角顶点A重合，点C、A、E在一条直线上，连接BD交AC于G，过点C作CM⊥BD于M，过点E作EF∥BD，直线CM与EF于点F，图1中CF与BD的数量关系还成立吗？若成立，请加以证明；若不成立，请说明你的理由．
查看习题详情和答案>>
把两个全等的含45°角的三角板按如图所示的位置放置，使B、A、D在一条直线上，C、A、E在一条直线上，过点C作CM⊥BD于M，过点E作EF∥BD；直线CM与EF相交于点F．
（1）求证：△CEF是等腰直角三角形．
猜想与发现
（2）在图1的条件下，CF与BD的数量关系为
CF=
BD
| 1 |
| 2 |
CF=
BD
．| 1 |
| 2 |
（3）如图2若把图1中Rt△ADE换为Rt△ABC不全等但相似的三角板时，其他条件不变，此时CF与BD的数量关系为
CF=
BD
| 1 |
| 2 |
CF=
BD
．| 1 |
| 2 |
拓展与探究
（4）如图3若将图1中的两块三角板换成任意两个全等的直角三角形（Rt△ABC≌Rt△DAE），使锐角顶点A重合，点C、A、E在一条直线上，连接BD交AC于G，过点C作CM⊥BD于M，过点E作EF∥BD，直线CM与EF于点F，图1中CF与BD的数量关系还成立吗？若成立，请加以证明；若不成立，请说明你的理由．
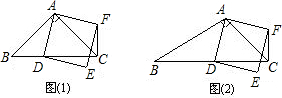CD=x，求线段CP的长．（用含x的式子表示）