题目内容
(2013•临汾二模)操作与证明
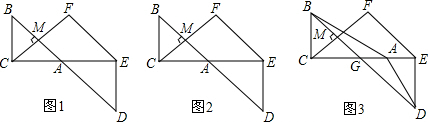
把两个全等的含45°角的三角板按如图所示的位置放置,使B、A、D在一条直线上,C、A、E在一条直线上,过点C作CM⊥BD于M,过点E作EF∥BD;直线CM与EF相交于点F.
(1)求证:△CEF是等腰直角三角形.
猜想与发现
(2)在图1的条件下,CF与BD的数量关系为
(3)如图2若把图1中Rt△ADE换为Rt△ABC不全等但相似的三角板时,其他条件不变,此时CF与BD的数量关系为
拓展与探究
(4)如图3若将图1中的两块三角板换成任意两个全等的直角三角形(Rt△ABC≌Rt△DAE),使锐角顶点A重合,点C、A、E在一条直线上,连接BD交AC于G,过点C作CM⊥BD于M,过点E作EF∥BD,直线CM与EF于点F,图1中CF与BD的数量关系还成立吗?若成立,请加以证明;若不成立,请说明你的理由.
把两个全等的含45°角的三角板按如图所示的位置放置,使B、A、D在一条直线上,C、A、E在一条直线上,过点C作CM⊥BD于M,过点E作EF∥BD;直线CM与EF相交于点F.
(1)求证:△CEF是等腰直角三角形.
猜想与发现
(2)在图1的条件下,CF与BD的数量关系为
CF=
BD
| 1 |
| 2 |
CF=
BD
.| 1 |
| 2 |
(3)如图2若把图1中Rt△ADE换为Rt△ABC不全等但相似的三角板时,其他条件不变,此时CF与BD的数量关系为
CF=
BD
| 1 |
| 2 |
CF=
BD
.| 1 |
| 2 |
拓展与探究
(4)如图3若将图1中的两块三角板换成任意两个全等的直角三角形(Rt△ABC≌Rt△DAE),使锐角顶点A重合,点C、A、E在一条直线上,连接BD交AC于G,过点C作CM⊥BD于M,过点E作EF∥BD,直线CM与EF于点F,图1中CF与BD的数量关系还成立吗?若成立,请加以证明;若不成立,请说明你的理由.

分析:(1)求出∠F=90°,∠FCE=45°,求出CF=EF,根据等腰直角三角形的判定推出即可.
(2)根据直角三角形斜边上中线性质得出CM=
AB=
CF,推出CF=BD,求出AD=AB,即可得出答案.
(3)设CM=a,EF=CF=x,由勾股定理求出CE=
x,AC=
a,求出AE=DE=
x-
a,在Rt△AED中,由勾股定理求出AD=
(
x-
a),即可求出答案.
(4)过E作EN⊥BD于N,推出FM=EN,求出EN=
GD,推出△BCG是等腰直角三角形,求出CM=
BG,即可求出答案.
(2)根据直角三角形斜边上中线性质得出CM=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设CM=a,EF=CF=x,由勾股定理求出CE=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(4)过E作EN⊥BD于N,推出FM=EN,求出EN=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:在△ABC中,AC=BC,CM⊥AB,∠ACB=90°
∴∠CMA=90°,∠ACF=
∠ACB=45°,
∵BD∥EF,
∴F=∠CMA=90°,
∴∠FEC=45°=∠FCE,
∴CF=EF,
即△CEF是等腰直角三角形;
(2)CF=
BD,
证明:∵△ACB≌△AED,
∴AD=AB=
BD,CA=AE,
∵EF∥AB,
∴CM=
CF,
∵BM=AM,∠ACB=90°,
∴CM=
AB,
∴AB=CF=
BD,
故答案为:CF=
BD;
(3)CF=
BD,
证明:设CM=a,EF=CF=x,
则由勾股定理得:CE=
x,
∵∠ACB=90°,AM=BM,
∴AB=2CM=2a,AM=CM=a,
由勾股定理得:AC=
a,
AE=DE=
x-
a,
在Rt△AED中,由勾股定理得:AD=
(
x-
a),
∴BD=AB+AD=2a+
(
x-
a)=2x
即CF=
BD,
故答案为:CF=
BD;
(4)成立,
证明:过E作EN⊥BD于N,
则EN∥FM,
∵DB∥EF,
∴EN=FM,
∵△ABC≌△DAE,
∴∠1=∠2,AB=DA,
∴∠ABD=∠4,
∴∠1+∠ABD=∠2+∠4,
∵∠5=∠1+∠ABD,
∴∠5=∠EDG,
∵∠DEA=90°,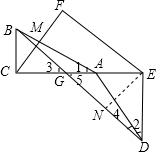
∴△GED是等腰直角三角形,
∵EN⊥DG,
∴EN=
GD,
∵在Rt△BCG中,∠3=∠5=45°,
∴△BCG是等腰直角三角形,
∵CM⊥BG,
∴CM=
BG,
∴CF=CM+FM=
BG+EN=
BG+
GD=
BD.
∴∠CMA=90°,∠ACF=
| 1 |
| 2 |
∵BD∥EF,
∴F=∠CMA=90°,
∴∠FEC=45°=∠FCE,
∴CF=EF,
即△CEF是等腰直角三角形;
(2)CF=
| 1 |
| 2 |
证明:∵△ACB≌△AED,
∴AD=AB=
| 1 |
| 2 |
∵EF∥AB,
∴CM=
| 1 |
| 2 |
∵BM=AM,∠ACB=90°,
∴CM=
| 1 |
| 2 |
∴AB=CF=
| 1 |
| 2 |
故答案为:CF=
| 1 |
| 2 |
(3)CF=
| 1 |
| 2 |

证明:设CM=a,EF=CF=x,
则由勾股定理得:CE=
| 2 |
∵∠ACB=90°,AM=BM,
∴AB=2CM=2a,AM=CM=a,
由勾股定理得:AC=
| 2 |
AE=DE=
| 2 |
| 2 |
在Rt△AED中,由勾股定理得:AD=
| 2 |
| 2 |
| 2 |
∴BD=AB+AD=2a+
| 2 |
| 2 |
| 2 |
即CF=
| 1 |
| 2 |
故答案为:CF=
| 1 |
| 2 |
(4)成立,
证明:过E作EN⊥BD于N,
则EN∥FM,
∵DB∥EF,
∴EN=FM,
∵△ABC≌△DAE,
∴∠1=∠2,AB=DA,
∴∠ABD=∠4,
∴∠1+∠ABD=∠2+∠4,
∵∠5=∠1+∠ABD,
∴∠5=∠EDG,
∵∠DEA=90°,

∴△GED是等腰直角三角形,
∵EN⊥DG,
∴EN=
| 1 |
| 2 |
∵在Rt△BCG中,∠3=∠5=45°,
∴△BCG是等腰直角三角形,
∵CM⊥BG,
∴CM=
| 1 |
| 2 |
∴CF=CM+FM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了全等三角形的性质,直角三角形斜边上中线性质,等腰直角三角形性质的判定的应用,题目比较典型,但是难度偏大.

练习册系列答案
相关题目

 (2013•临汾二模)把一个含30°的直角三角板和一把直尺按如图所示的位置放置,若∠1=20°,则∠2的度数是( )
(2013•临汾二模)把一个含30°的直角三角板和一把直尺按如图所示的位置放置,若∠1=20°,则∠2的度数是( ) (2013•临汾二模)如图所示的平面图是4×4方格,若向方格面掷飞镖,飞镖落在黑色区域的概率为( )
(2013•临汾二模)如图所示的平面图是4×4方格,若向方格面掷飞镖,飞镖落在黑色区域的概率为( ) (2013•临汾二模)如图,在四边形ABCD中,对角线AC、BD相交于点O,若AO=C0=BO=DO,AC⊥BD,则四边形ABCD的形状是( )
(2013•临汾二模)如图,在四边形ABCD中,对角线AC、BD相交于点O,若AO=C0=BO=DO,AC⊥BD,则四边形ABCD的形状是( )