摘要:[解析]考察了相似的两种基本图形.平行四边形中利用全等三角形的简单证明. [答案](1) AEH与DFH.(或AEH与BEG. 或BEG与CFG .或DFH与CFG) (2)OE=OF. 证明:四边形ABCD是平行四边形. ∥CD. . . △△. .
网址:http://m.1010jiajiao.com/timu3_id_478883[举报]
为了测量一池塘的两端A,B之间的距离,同学们想出了如下的两种方案:

①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;
②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即是AB的距离.
问:
(1)方案①是否可行?
(2)方案②是否可行?
(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要
查看习题详情和答案>>

①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;
②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即是AB的距离.
问:
(1)方案①是否可行?
可行
可行
,理由是SAS可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED
SAS可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED
;(2)方案②是否可行?
可行
可行
,理由是ASA可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED
ASA可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED
;(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要
AB∥DE
AB∥DE
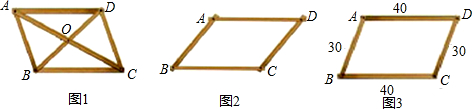
就可以了,请把小明所说的条件补上.(1)小明的爸爸在钉制平行四边形框架时,采用了下面的两种方法.
方法一:如图1,将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
这样做的依据是:
方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
(2)2002年世界数学家大会(ICM-2002)在北京召开,这节大会的会标的中央图案是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!在这个“弦图”中,隐含着我们学过的一个重要的数学定理,这个定理可以用含a、b、c的等式来表示,它是:

查看习题详情和答案>>
方法一:如图1,将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
对角线互相平分的四边形是平行四边形
对角线互相平分的四边形是平行四边形
.方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
这样做的依据是:
一组对边平行且相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
.方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
两组对边分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
.
(2)2002年世界数学家大会(ICM-2002)在北京召开,这节大会的会标的中央图案是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!在这个“弦图”中,隐含着我们学过的一个重要的数学定理,这个定理可以用含a、b、c的等式来表示,它是:
a2+b2=c2
a2+b2=c2
.
18、“在一次考试中,考生有2万多名,如果为了得到这些考生的数学成绩的平均水平,若将他们的成绩全部相加再除以考生的总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学平均成绩呢”“通常,在考生很多的情况下,我们是从中抽取部分考生(比如500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.”
在上述文字表述中,提到了调查的两种方式是
查看习题详情和答案>>
在上述文字表述中,提到了调查的两种方式是
抽样调查
和全面调查
;反映了用样本估计总体的数学思想,其中,总体是2万多名考生的数学平均成绩
,样本是500名考生的数学平均成绩
,请用较简洁的语言,举一个在实际生活中,运用同种思想解决问题的例子,写在下面:为了了解某市1万多名初三毕业生的数学平均成绩,从中抽取500名考生的数学成绩,用他们的平均成绩去估计所有考生的平均成绩.
.19、在一次考试中,考生有2万多名,如果为了得到这些考生的数学成绩的平均水平,若将他们的成绩全部相加再除以考生的总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学,平均成绩呢?
通常,在考生很多的情况下,我们是从中抽取部分考生(比如500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.在上述文字表述中,提到了调查的两种方式是
查看习题详情和答案>>
通常,在考生很多的情况下,我们是从中抽取部分考生(比如500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.在上述文字表述中,提到了调查的两种方式是
全面调查
和抽样调查
;反映了用样本估计总体的数学思想.其中,总体是2万多名考生的数学平均成绩的全体
,样本是从中抽取的部分考生的数学平均成绩
,请用较简洁的语言,举一个在实际生活中,运用同种思想解决问题的例子,写在下面:比如中央电视台要想调查北京观众对《星光大道》节目的收视率,从北京的不同地方,不同层次,不同年龄段,不同文化背景的观众中共抽取10000名观众加以调查,用他们的收视率来代表北京市所有市民对节目的收视率.
.