题目内容
(1)小明的爸爸在钉制平行四边形框架时,采用了下面的两种方法.
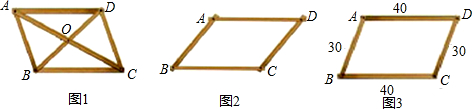
方法一:如图1,将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
这样做的依据是:
方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
(2)2002年世界数学家大会(ICM-2002)在北京召开,这节大会的会标的中央图案是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!在这个“弦图”中,隐含着我们学过的一个重要的数学定理,这个定理可以用含a、b、c的等式来表示,它是:

方法一:如图1,将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
对角线互相平分的四边形是平行四边形
对角线互相平分的四边形是平行四边形
.方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
这样做的依据是:
一组对边平行且相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
.方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.这样做的依据是:
两组对边分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
.
(2)2002年世界数学家大会(ICM-2002)在北京召开,这节大会的会标的中央图案是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!在这个“弦图”中,隐含着我们学过的一个重要的数学定理,这个定理可以用含a、b、c的等式来表示,它是:
a2+b2=c2
a2+b2=c2
.
分析:(1)利用平行四边形的判定方法分别判断得出所用定理即可;
(2)通过图中三角形面积、正方形面积之间的关系,证明勾股定理.
(2)通过图中三角形面积、正方形面积之间的关系,证明勾股定理.
解答:解:(1)方法一:如图1,将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.
得出AO=CO,DO=BO,则四边形ABCD就是平行四边形,
故这样做的依据是:对角线互相平分的四边形是平行四边形.
方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
得出AB
CD,则四边形ABCD就是平行四边形,
故这样做的依据是:一组对边平行且相等的四边形是平行四边形.
方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.得出:AB=CD,AD=BC,则四边形ABCD就是平行四边形.
这样做的依据是:两组对边分别相等的四边形是平行四边形;
故答案为:对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;
(2)如图:大正方形的面积=c2,
用三角形的面积与边长为(b-a)的正方形的面积表示为4×
ab+(b-a)2,
即c2=4×
ab+(b-a)2,化简得a2+b2=c2.
故答案为:a2+b2=c2.
得出AO=CO,DO=BO,则四边形ABCD就是平行四边形,
故这样做的依据是:对角线互相平分的四边形是平行四边形.
方法二:如图2,将两根同样长的木条AB、CD平行放置,再木条AD、BC加固,则四边形ABCD就是平行四边形.
得出AB
| ∥ |
. |
故这样做的依据是:一组对边平行且相等的四边形是平行四边形.
方法三:如图3,用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边,并把相等的木条作为相对的边用钉子固定,则四边形ABCD就是平行四边形.得出:AB=CD,AD=BC,则四边形ABCD就是平行四边形.
这样做的依据是:两组对边分别相等的四边形是平行四边形;
故答案为:对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;
(2)如图:大正方形的面积=c2,
用三角形的面积与边长为(b-a)的正方形的面积表示为4×
| 1 |
| 2 |
即c2=4×
| 1 |
| 2 |
故答案为:a2+b2=c2.
点评:此题主要考查了平行四边形的判定和用数形结合来证明勾股定理,熟练掌握平行四边形的判定是解题关键.

练习册系列答案
相关题目
 1、如图,小明的爸爸在院子的门板上钉了一个加固板,从数学的角度看,这样做的道理是
1、如图,小明的爸爸在院子的门板上钉了一个加固板,从数学的角度看,这样做的道理是