摘要:[解析]要想证明△ABC与△SBR相似.只要证明其中的两个角相等即可,要想得到TS=PA.只要证明△TPS≌△PFA即可,对于(3).需要建立正方形PTEF的面积y与AP的函数关系式.利用函数的极值来解决. [答案]解:(1)∵RS是直角∠PRB的平分线.∴∠PRS=∠BRS=45°. 在△ABC与△SBR中.∠C=∠BRS=45°.∠B是公共角. ∴△ABC∽△SBR.. (2)线段TS的长度与PA相等. ∵四边形PTEF是正方形. ∴PF=PT.∠SPT+∠FPA=180°-∠TPF=90°, 在Rt△PFA中.∠PFA +∠FPA=90°, ∴∠PFA=∠TPS. ∴Rt△PAF≌Rt△TSP.∴PA=TS. 当点P运动到使得T与R重合时. 这时△PFA与△TSP都是等腰直角三角形且底边相等.即有PA=TS. 由以上可知.线段ST的长度与PA相等. (3)由题意.RS是等腰Rt△PRB的底边PB上的高. ∴PS=BS, ∴BS+PS+PA=1, ∴PS=. 设PA的长为x.易知AF=PS. 则y=PF=PA+PS,得y=x+(), 即y=. 根据二次函数的性质.当x=时.y有最小值为. 如图2.当点P运动使得T与R重合时.PA=TS为最大. 易证等腰Rt△PAF≌等腰Rt△PSR≌等腰Rt△BSR. ∴PA=. 如图3.当P与A重合时.得x=0. ∴x的取值范围是0≤x≤. ∴①当x的值由0增大到时.y的值由减小到 ∴②当x的值由增大到时.y的值由增大到 ∵≤≤.∴在点P的运动过程中. 正方形PTEF面积y的最小值是.y的最大值是.
网址:http://m.1010jiajiao.com/timu3_id_478785[举报]
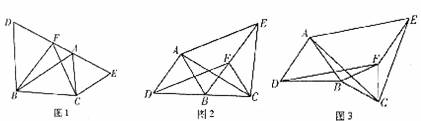
如图1,点D、F、A、E在同一直线上,且AE=DF,分别以DA、AE为一边,在直线DE
的同侧作等边△DBA和等边△ACE,试证明△BCF也是等边三角形。
(1)下面是小伟对此题的分析过程,请你根据他的分析填空:此题中,要想证明△BCF是等边三角形,至少要证明两条边相等。欲证两条边相等,可以通过证明这两条边所在的两个三角形全等来实现。根据已知条件,在不加辅助线的情况下,不妨尝试证明 ≌△ABC,依据是 (写出定义、公理或定理的内容);
(2)如图2,点D、B、C在同一直线上,分别以DB、BC为一边,在直线DC的同侧作等边△DBA和等边△BCF,再以DA、DF为邻边作□ADFE,求证:△ACE是等边三角形;
(3)如图3是将(2)中的等边△BCF绕点B顺时针旋转一个角度后得到的图形,若其他条件不变,△ACE是否还是等边三角形?请加以说明。
 如图,A是BD的中点,△ABC和△ADE均为等边三角形,则要想由△ABC得到△ADE,( )
如图,A是BD的中点,△ABC和△ADE均为等边三角形,则要想由△ABC得到△ADE,( )
 已知,如图,AB⊥AC,DC⊥BD,要想使△ABC≌△DBC,小东添加了一个条件AB=CD,他判断全等的依据是
已知,如图,AB⊥AC,DC⊥BD,要想使△ABC≌△DBC,小东添加了一个条件AB=CD,他判断全等的依据是