摘要: 如图12.直线与两坐标轴分别相交于A.B点.点M是线段AB上任意一点.过M分别作MC⊥OA于点C.MD⊥OB于D. (1)当点M在AB上运动时.你认为四边形OCMD的周长是否发生变化?并说明理由, (2)当点M运动到什么位置时.四边形OCMD的面积有最大值?最大值是多少? (3)当四边形OCMD为正方形时.将四边形OCMD沿着x轴的正方向移动.设平移的距离为.正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象. 52. 如图11.在△ABC中.∠C=90°.BC=8.AC=6.另有一直角梯形DEFH (HF∥DE.∠HDE=90°)的底边DE落在CB上.腰DH落在CA上.且DE=4.∠DEF=∠CBA.AH∶AC=2∶3 (1)延长HF交AB于G.求△AHG的面积. (2)操作:固定△ABC.将直角梯形DEFH以每秒1个 单位的速度沿CB方向向右移动.直到点D与点B 重合时停止.设运动的时间为t秒.运动后的直角梯 形为DEFH′. 探究1:在运动中.四边形CDH′H能否为正方形?若能. 请求出此时t的值,若不能.请说明理由. 探究2:在运动过程中.△ABC与直角梯形DEFH′重叠 部分的面积为y.求y与t的函数关系.?
网址:http://m.1010jiajiao.com/timu3_id_478242[举报]
 如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.(1)求直线PQ的解析式;
(2)问在线段PQ上是否存在点A使长方形ABOC的面积为
| 3 | 4 |
 如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
(1)求直线PQ的解析式;
(2)问在线段PQ上是否存在点A使长方形ABOC的面积为 ?若存在,请直接写出点A的坐标;若不存在,说明理由.
?若存在,请直接写出点A的坐标;若不存在,说明理由.
查看习题详情和答案>>
在平面直角坐标系中,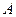 点坐标为
点坐标为 ,
,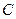 点坐标为
点坐标为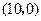 .
.
(1)如图①,若直线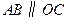 ,
,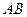 上有一动点
上有一动点 ,当
,当 点的坐标为 时,有
点的坐标为 时,有 ;
;
(2)如图②,若直线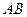 与
与 不平行,在过点
不平行,在过点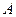 的直线
的直线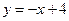 上是否存在点
上是否存在点 ,使
,使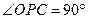 ,若有这样的点
,若有这样的点 ,求出它的坐标.若没有,请简要说明理由.
,求出它的坐标.若没有,请简要说明理由.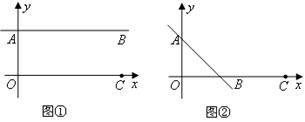
 点坐标为
点坐标为 ,
, 点坐标为
点坐标为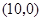 .
.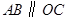 ,
, 上有一动点
上有一动点 ,当
,当 ;
; 不平行,在过点
不平行,在过点 上是否存在点
上是否存在点 ,若有这样的点
,若有这样的点