摘要：利用归纳法.通过观察.猜想.推理.总结规律.得到结论.以考察学生的观察.创新能力.应特别注意了高中知识(如:数列.排列.组合.虚数等)的渗透.例如:1.A1.A2.A3.A4四个舞蹈演员.在舞台上跳舞.面对观众作队列变化.其变化 规律是:一个舞蹈演员 A1面对观众跳舞的变化种类是:A1 为1种, 二个舞蹈演员 A1..A2面对观众跳舞的队形排列的变化种类是:A1A2,A2A1为2 种, 三个舞蹈演员 A1..A2.A3面对观众跳舞的队形排列的变化种类是:A1A2A3, A1A3A2,A2A3A1,A2A1A3,A3A1A2,A3A2A1为6种, 四个舞蹈演员 A1..A2.A3.A4面对观众跳舞的队形排列的变化种数为 种.
网址：http://m.1010jiajiao.com/timu3_id_478049[举报]
探索研究：已知A，B在数轴上分别表示a、b．利用数形结合思想回答下列问题：
（1）填写下表：
| 数 | 列A | 列B | 列C | 列D | 列E | 列F |
| a | 5 | -5 | -6 | -6 | -10 | -2.5 |
| b | 3 | 0 | 4 | -4 | 2 | -2.5 |
| A，B两点的距离 | 2 | 10 | 5 |
|x+2|
|x+2|
．（3）若A，B两点的距离为d，则d与a、b有何数量关系：
d=|a-b|
d=|a-b|
．（4）若x表示一个有理数，且-3＜x＜1，则|x-1|+|x+3|=
4
4
．探索与应用．
先填写下表，通过观察后再回答问题：
（1）表格中x=
（2）从表格中探究a与
数位的规律，并利用这个规律解决下面两个问题：
①已知
≈3.16，则
≈
②已知
=1.8，若
=180，则a=
查看习题详情和答案>>
先填写下表，通过观察后再回答问题：
| a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … | ||
|
… | 0.01 | x | 1 | y | 100 | … |
0.1
0.1
；y=10
10
；（2）从表格中探究a与
| a |
①已知
| 10 |
| 1000 |
31.6
31.6
；②已知
| 3.24 |
| a |
32400
32400
．
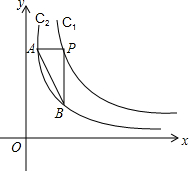如图：已知反比例C1：y=| k1 |
| x |
| k2 |
| x |
（1）当取k1=4，k2=1，
①点P坐标为（2，2）时，则S三角形ABP=
| 9 |
| 8 |
| 9 |
| 8 |
②点P坐标为（1，4）时，S三角形ABP=
| 9 |
| 8 |
| 9 |
| 8 |
（2）通过观察、思考（1）的计算结果，你能猜想到△ABP的面积有何规律或特征？并请你用含k1、k2的代数式表示△ABP的面积．
我国古籍《周髀算经》中早有记载“勾三股四弦五”，下面我们来探究两类特殊的勾股数．
（1）通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：
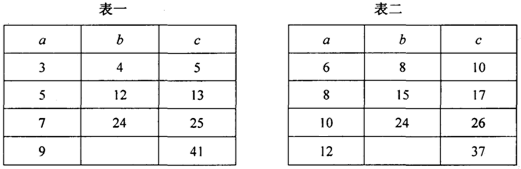
（2）我们发现，表一中a为大于l的奇数，此时b、c的数量关系是
（3）一般地，对于表一，用含a的代数式表示b=
；对于表二，用含a的代数式表示b=
-1
-1；
（4）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，l2，13”与表二中的“10，24，26”恰好也成倍数关系…．请直接利用这一规律计算：在Rt△ABC中，当a=
，b=
时，斜边c的值．
查看习题详情和答案>>
（1）通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：
（2）我们发现，表一中a为大于l的奇数，此时b、c的数量关系是
b+1=c
b+1=c
；表二中a为大于4的偶数，此时b、c的数量关系是b+2=c
b+2=c
；（3）一般地，对于表一，用含a的代数式表示b=
| a2-1 |
| 2 |
| a2-1 |
| 2 |
| a2 |
| 4 |
| a2 |
| 4 |
（4）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，l2，13”与表二中的“10，24，26”恰好也成倍数关系…．请直接利用这一规律计算：在Rt△ABC中，当a=
| 3 |
| 5 |
| 4 |
| 5 |