网址：http://m.1010jiajiao.com/timu3_id_473952[举报]
经过点A（－3，1）、B（0，－2），将该直线向右平移2个单位得到直线
。
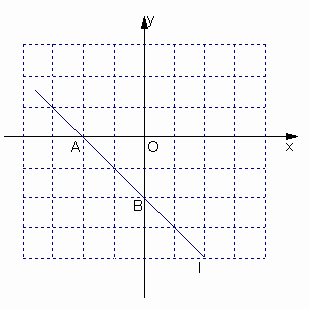
在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点A（0，2），C（－1，0），如图所示.
（1）求点B的坐标；
（2）若以（
）为顶点的抛物线经过点B，求该抛物线的解析式；
（3）在（2）中的抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由.
 |
查看习题详情和答案>>
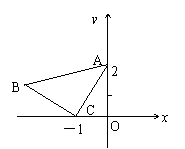
如图，在平面直角坐标系中放置一直角三角板，其顶点为A(－1，0)，
，O(0，0)，将此三角板绕原点O顺时针旋转90°，得到
．
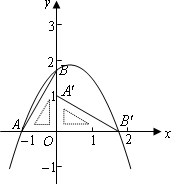
(1)如图，一抛物线经过点
，求该抛物线解析式；
(2)设点P是在第一象限内抛物线上一动点，求使四边形
的面积达到最大时点P的坐标及面积的最大值．
已知二次函数y＝a(x2－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．
(1)如图①，连接AC，将△OAC沿直线AC翻折，若点O的对应点O'恰好落在该抛物线的对称轴上，求实数a的值；
(2)如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．”若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；
(3)如图②，当点P在抛物线对称轴上时，设点P的纵坐标t是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．
的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为
，折痕为EF．
∥x轴时，求点
和E的坐标．
x2＋bx＋0经过点
和A时，求该抛物线与x轴的交点坐标．
在OB上运动但不与点O、B重合时，能否使△
成为直角三角形？若能，请求出此时点
的坐标；若不能，请你说明理由．