摘要: 如图①.在平面直角坐标系中.直线分别交轴.轴于.两点.将射线绕着点顺时针旋转得到射线.点为上的动点.点为上的动点.点在的内部. ⑴求线段的长, ⑵当∥轴.且四边形为梯形时.求△的面积, ⑶求△周长的最小值, ⑷当△的周长取得最小值.且时.△的面积为 (第⑷问需填写结论.不要求书写) 备用图
网址:http://m.1010jiajiao.com/timu3_id_473347[举报]
(本题满分12分)
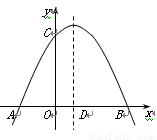
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为![]() 秒(
秒(![]() ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的![]() ?若存在,求出
?若存在,求出![]()
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求![]() 的值或
的值或![]() 的取值范围
的取值范围
查看习题详情和答案>>
(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,
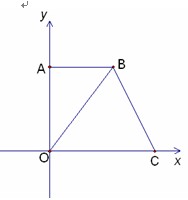
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为 秒(
秒(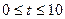 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的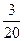 ?若存在,求出
?若存在,求出
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求 的值或
的值或 的取值范围
查看习题详情和答案>>
的取值范围
查看习题详情和答案>>
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,

(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为
 秒(
秒(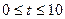 ),
),①是否存在某个时刻,使△OPH的面积等于△OBC面积的
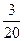 ?若存在,求出
?若存在,求出
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求
 的值或
的值或 的取值范围
查看习题详情和答案>>
的取值范围
查看习题详情和答案>>
(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,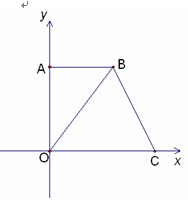
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为 秒(
秒(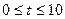 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的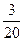 ?若存在,求出
?若存在,求出
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求 的值或
的值或 的取值范围
的取值范围

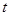 秒(
秒(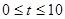 ),
),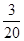 ?若存在,求出
?若存在,求出