题目内容
(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,

(1) 求点B的坐标;
(2)
点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为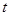 秒(
秒(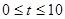 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的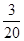 ?若存在,求出
?若存在,求出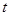
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求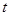 的值或
的值或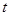 的取值范围
的取值范围
【答案】
(1)B(6,8)
(2)①7
②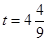 或
或 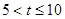
【解析】(1)B(6,8)
(2)①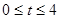 时 ,
时 ,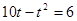 ,
,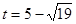 (
( 舍去);
舍去);
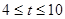 时 ,
时 ,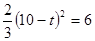 ,
,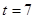 (
(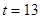 舍去);
舍去);
②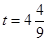 或
或 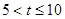
第1问2分,第2问6分,第3问4分

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目


 分别交
分别交 轴,
轴, 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形. 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作 ,垂足为H,连接
,垂足为H,连接 ,
, .设点P的运动时间为
.设点P的运动时间为 秒.
秒. 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.

 =4
=4 ,求△ABC的周长.
,求△ABC的周长. 、
、 (千米)与行驶时间
x(时)的关系如图②所示.
(千米)与行驶时间
x(时)的关系如图②所示. 
 ,乙的速度为
,乙的速度为