摘要:在平面直角坐标系中.点关于原点对称的点是( ) A. B. C. D. 2已知点与点关于轴对称.则 . . 考点三 用坐标确定位置. 例题已知坐标平面上的机器人接受指令“[a.A] (a≥0.0°<A<180°)后的行动结果为:在原地顺时针旋转A后.再向面对方向沿直线行走a. 若机器人的位置在原点.面对方向为y轴的负半轴.则它完成一次指令[2.60°]后.所在位置的坐标为( ) A. (-1.-) B. (-1.) C.(.-1) D.(-.-1) 思路点拨:坐标系上的任意点与它的坐标一一对应.因此可以用坐标确定点的位置.反过来点移动到任意位置都有与它对应的坐标.解决这类问题的关键就是弄清楚图形的特征和图形变换的特征.找出它的位置.在确定其坐标. 解析,如土所示.过M作由题目中所给信息.OM=2. .所以..所以 由勾股定理.... .因为M点在第三象限.所以.选D 规律总结:要抓住题目中的图形的变化规则.确定所在位置.再求出点的坐标. [针对训练]
网址:http://m.1010jiajiao.com/timu3_id_470639[举报]
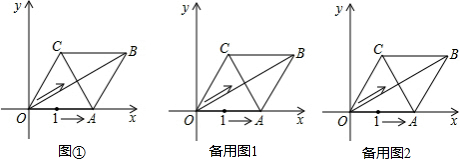
如图①,在平面直角坐标系中,点A从点(1,0)出发以每秒1个单位长度的速度沿x轴向右运动,在运动过程中,以OA为一边作菱形OABC,使B、C在第一象限,且∠AOC=60°,连接AC、OB;同时点M从原点O出发,以每秒
个单位长度的速度沿对角线OB向点B运动,若以点M为圆心,MA的长为半径画圆,设运动时间为t秒.
(1)当t=1时,判断点O与⊙M的位置关系,并说明理由.
(2)当⊙M与OC边相切时,求t的值.
(3)随着t的变化,⊙M和菱形OABC四边的公共点个数也在变化,请直接写出公共点个数与t的大小之间的对应关系.
查看习题详情和答案>>
| 3 |
(1)当t=1时,判断点O与⊙M的位置关系,并说明理由.
(2)当⊙M与OC边相切时,求t的值.
(3)随着t的变化,⊙M和菱形OABC四边的公共点个数也在变化,请直接写出公共点个数与t的大小之间的对应关系.

 (2011•黔西南州)如图,在平面直角坐标系中,点A的坐标为(-6,0),以点A为圆心的圆交x轴于O、B两点,直线y=
(2011•黔西南州)如图,在平面直角坐标系中,点A的坐标为(-6,0),以点A为圆心的圆交x轴于O、B两点,直线y=| 3 |
| 4 |
(1)求抛物线的解析式;
(2)判断直线CD与⊙A的位置关系,并说明理由;
(3)若点M以每秒4个单位长度的速度由点B沿x轴向点C运动,点N以每秒1个单位长度的速度由点C沿直线y=
| 3 |
| 4 |
(4)在抛物线上是否存在点P,使△APC的面积是△BCD面积的
| 5 |
| 8 |
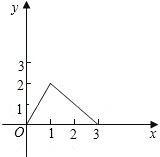 如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.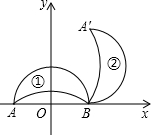 如右图所示,在平面直角坐标系中,点A、B的坐标分别为(-4,0)和(4,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为
如右图所示,在平面直角坐标系中,点A、B的坐标分别为(-4,0)和(4,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为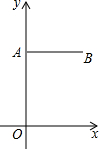 如图,在平面直角坐标系中,点A(0,8),点B(6,8).
如图,在平面直角坐标系中,点A(0,8),点B(6,8).