题目内容
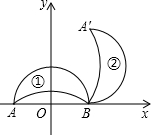如右图所示，在平面直角坐标系中，点A、B的坐标分别为（-4，0）和（4，0）．月牙①绕点B顺时针旋转90°得到月牙②，则点A的对应点A′的坐标为（4，8）
（4，8）
．分析：连接A′B，根据点A、B的坐标求出AB的长，再根据旋转的性质可得A′B⊥x轴，A′B=AB，然后写出点A′坐标即可．
解答：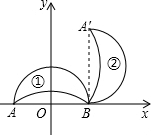
解：如图，连接A′B，
∵点A、B的坐标分别为（-4，0）和（4，0），
∴AB=4-（-4）=4+4=8，
∵月牙①绕点B顺时针旋转90°得到月牙②，
∴A′B⊥x轴，A′B=AB，
∴A′的坐标为（4，8）．
故答案为：（4，8）．
解：如图，连接A′B，∵点A、B的坐标分别为（-4，0）和（4，0），
∴AB=4-（-4）=4+4=8，
∵月牙①绕点B顺时针旋转90°得到月牙②，
∴A′B⊥x轴，A′B=AB，
∴A′的坐标为（4，8）．
故答案为：（4，8）．
点评：本题考查了坐标与图形变化-旋转，熟记旋转的性质，求出A′B与x轴的关系和长度是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
