摘要:如图3.已知△ABC与△ADE中.则∠C=∠E, ∠DAB=∠CAE,则下列各式成立的个数是( ). ∠D=∠B ,= , = , = A.1个 B.2个 C.3个 D.4个
网址:http://m.1010jiajiao.com/timu3_id_470501[举报]
(1)探究新知:
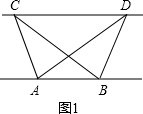
如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
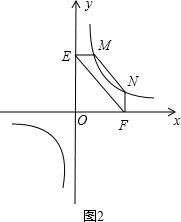
①如图2,点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试证明:MN∥EF.
 查看习题详情和答案>>
查看习题详情和答案>>
如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:
①如图2,点M,N在反比例函数y=
| k | x |
试证明:MN∥EF.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)探究归纳:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:①如图2,点M,N在反比例函数y=
(k>0,x>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
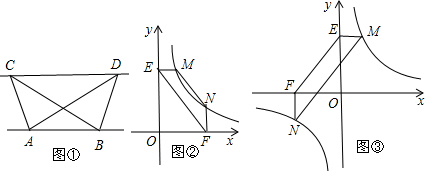
②如图3,点M,N在反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.
查看习题详情和答案>>
(2)结论应用:①如图2,点M,N在反比例函数y=
| k |
| x |

②如图3,点M,N在反比例函数y=
| 10 |
| x |
| 10 |
| x |
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
①如图2,点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F,试证明:MN∥EF;
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.
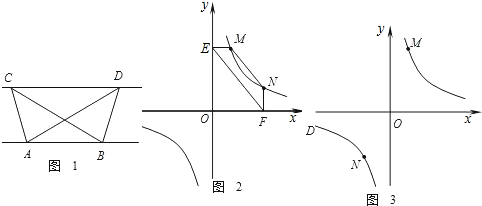 查看习题详情和答案>>
查看习题详情和答案>>
(2)结论应用:
①如图2,点M,N在反比例函数y=
| k | x |
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:如图2,点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(3)变式探究:如图3,点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H.试证明:EF∥GH.

查看习题详情和答案>>
(2)结论应用:如图2,点M,N在反比例函数y=
| k |
| x |
(3)变式探究:如图3,点M,N在反比例函数y=
| k |
| x |

如图1,已知△ABC与△DCE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,点D在AC上,直线BD交AE于点F.
(1)请补充完整证明“BD=AE,BF⊥AE”的推理过程;
证明:在△ACE与△BCD中
∵(
∴△ACE≌△BCD(SAS)
∴BD=AE,∠CAE=∠CBD(全等三角形的对应角相等)
∵∠ACE=90°
∴∠CAE+∠AEC=90°(
∴∠CBD+∠AEC=90°(等量代换)
∴
∴BF⊥AE(垂直的定义)
(2)将△DCE绕着点C旋转,在旋转过程中保持△DCE的大小与形状均不变,那么,当△DCE旋转至图2的位置时,(1)中的结论是否仍然成立?为什么?

查看习题详情和答案>>
(1)请补充完整证明“BD=AE,BF⊥AE”的推理过程;
证明:在△ACE与△BCD中
∵(
AC=BC,∠DCB=∠ECA,DC=EC
AC=BC,∠DCB=∠ECA,DC=EC
)∴△ACE≌△BCD(SAS)
∴BD=AE,∠CAE=∠CBD(全等三角形的对应角相等)
∵∠ACE=90°
∴∠CAE+∠AEC=90°(
直角三角形的两锐角互余
直角三角形的两锐角互余
)∴∠CBD+∠AEC=90°(等量代换)
∴
∠BFE=90°
∠BFE=90°
∴BF⊥AE(垂直的定义)
(2)将△DCE绕着点C旋转,在旋转过程中保持△DCE的大小与形状均不变,那么,当△DCE旋转至图2的位置时,(1)中的结论是否仍然成立?为什么?
