题目内容
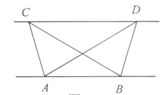
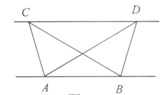
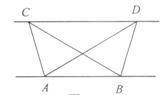
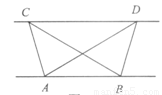
(1)探究归纳:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.(2)结论应用:①如图2,点M,N在反比例函数y=
| k |
| x |
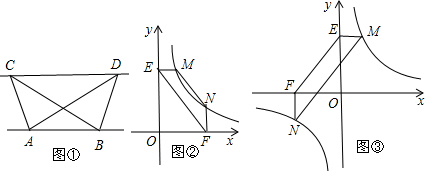
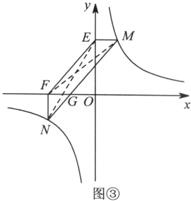
②如图3,点M,N在反比例函数y=
| 10 |
| x |
| 10 |
| x |
分析:(1)分别过点C、D作CG⊥AB、DH⊥AB,垂足为G、H,根据三角形的面积求出CG=DH,推出平行四边形CGDH即可
(2)②证△EMF和△NEF的面积相等,根据(1)即可推出答案;②设点M的坐标为(x1,y1),点N的坐标为(x2,y2),根据三角形的面积公式求出S△EFM=S△EFN,求出FN即可.
(2)②证△EMF和△NEF的面积相等,根据(1)即可推出答案;②设点M的坐标为(x1,y1),点N的坐标为(x2,y2),根据三角形的面积公式求出S△EFM=S△EFN,求出FN即可.
解答: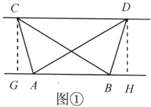 (1)证明:分别过点C、D作CG⊥AB、DH⊥AB,垂足为G、H,则∠CGA=∠DHB=90°.
(1)证明:分别过点C、D作CG⊥AB、DH⊥AB,垂足为G、H,则∠CGA=∠DHB=90°.
∵CG⊥AB、DH⊥AB,
∴∠CGA=∠DHA=90°,
∴∠CGA+∠DHA=180°,
∴CG∥DH.
∵△ABC与△ABD的面积相等,
∴CG=DH,
∴四边形CGHD为平行四边形,
∴AB∥CD.
(2)①证明:连接MF,NE,
设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∵点M,N在反比例函数y=
(k>0)的图象上,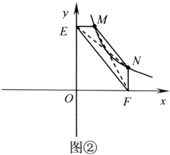
∴x1y1=k,x2y2=k,
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2,
∴S△EFM=
x1•y1=
k,S△EFN=
x2•y2=
k,
∴S△EFM=S△EFN,
由(1)中的结论可知:MN∥EF.
②解:连接FM、EN.
设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∴S△EFM=
EM•EO=
k=5,S△EFN=
FN•FO=
k=5,
∴S△EFM=S△EFN,
 由(1)中的结论可知:MN∥EF.
由(1)中的结论可知:MN∥EF.
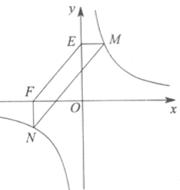
设MN和x轴的交点为G(如图③),
则四边形EFGM为平行四边形,EM=2.
S四边形EFNM=S平行四边形EFGM+S△FNG,
12=x1y1+
x1y2
=10+
×2×FN,
当S四边形EFNM=12时,y2=-FN=-2,代入y=
得:x2=-5,
∴点N的坐标为(-5,-2),
答:点N的坐标.是(-5,-2).
 (1)证明:分别过点C、D作CG⊥AB、DH⊥AB,垂足为G、H,则∠CGA=∠DHB=90°.
(1)证明:分别过点C、D作CG⊥AB、DH⊥AB,垂足为G、H,则∠CGA=∠DHB=90°.∵CG⊥AB、DH⊥AB,
∴∠CGA=∠DHA=90°,
∴∠CGA+∠DHA=180°,
∴CG∥DH.
∵△ABC与△ABD的面积相等,
∴CG=DH,
∴四边形CGHD为平行四边形,
∴AB∥CD.
(2)①证明:连接MF,NE,
设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∵点M,N在反比例函数y=
| k |
| x |

∴x1y1=k,x2y2=k,
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2,
∴S△EFM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EFM=S△EFN,
由(1)中的结论可知:MN∥EF.
②解:连接FM、EN.
设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∴S△EFM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EFM=S△EFN,
 由(1)中的结论可知:MN∥EF.
由(1)中的结论可知:MN∥EF.设MN和x轴的交点为G(如图③),
则四边形EFGM为平行四边形,EM=2.
S四边形EFNM=S平行四边形EFGM+S△FNG,
12=x1y1+
| 1 |
| 2 |
=10+
| 1 |
| 2 |
当S四边形EFNM=12时,y2=-FN=-2,代入y=
| 10 |
| x |
∴点N的坐标为(-5,-2),
答:点N的坐标.是(-5,-2).
点评:本题主要考查对平行四边形的性质和判定,三角形的面积,反比例函数图象上点的坐标特征等知识点的理解和掌握,能推出MN∥EF是解此题的关键.

练习册系列答案
相关题目
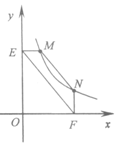
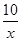 的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.
的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.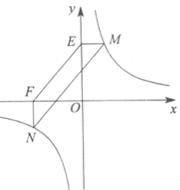
 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=
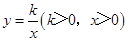 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.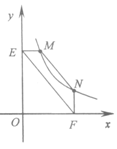
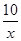 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=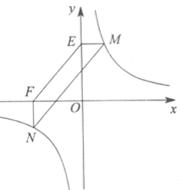
 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.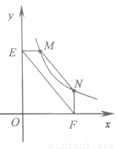
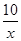 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=