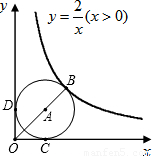
摘要:如图.点B坐标为(7.9) ⊙B的半径为3. AB⊥y轴.垂足为A.点P从A点出发沿射线AB运动.速度为每秒一个单位.设运动的时间t(s): (1)当点P运动到圆上时.求t值.并直接写出此时P点坐标. (2)若P运动12s时.判断直线OP与⊙B的位置关系.并说明你的理由. (3)点P从A点出发沿射线AB运动的过程中.请探究直线OP与⊙B有哪几种位置关系.并直接写出相应的运动时间t的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_468508[举报]
如图,点P在y轴上,⊙P交x轴于A,B两点,连接AP并延长交⊙P于C点,过点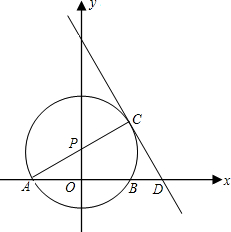 C的直线y=-2x+b交x轴于点D,交y轴于点E,且⊙P的半径为
C的直线y=-2x+b交x轴于点D,交y轴于点E,且⊙P的半径为
,AB=4.
(1)求点P,点C的坐标;
(2)求证:CD是⊙P的切线;
(3)若二次函数y=-
x2+mx+n的图象经过A,C两点,求这个二次函数的解析式,并写出使函数值大于一次函数y=-2x+b值的x的取值范围.
查看习题详情和答案>>
 C的直线y=-2x+b交x轴于点D,交y轴于点E,且⊙P的半径为
C的直线y=-2x+b交x轴于点D,交y轴于点E,且⊙P的半径为| 5 |
(1)求点P,点C的坐标;
(2)求证:CD是⊙P的切线;
(3)若二次函数y=-
| 1 |
| 2 |
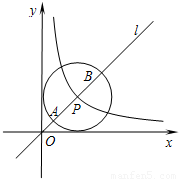
如图,点P是双曲线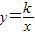 (x>0)上一点,以点P为圆心,2为半径的圆与直线y=x的交点为A、B.
(x>0)上一点,以点P为圆心,2为半径的圆与直线y=x的交点为A、B.
(1)当⊙P与x轴和y轴都相切时,求点P的坐标及双曲线的函数表达式;
(2)若点P在双曲线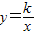 (x>0)上运动,当弦AB的长等于
(x>0)上运动,当弦AB的长等于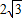 时,求点P的坐标.
时,求点P的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
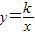 (x>0)上一点,以点P为圆心,2为半径的圆与直线y=x的交点为A、B.
(x>0)上一点,以点P为圆心,2为半径的圆与直线y=x的交点为A、B.(1)当⊙P与x轴和y轴都相切时,求点P的坐标及双曲线的函数表达式;
(2)若点P在双曲线
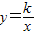 (x>0)上运动,当弦AB的长等于
(x>0)上运动,当弦AB的长等于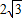 时,求点P的坐标.
时,求点P的坐标. 查看习题详情和答案>>
查看习题详情和答案>>
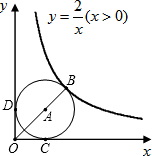 如图,点B是函数
如图,点B是函数 π时,求AB所在直线的函数解析式;
π时,求AB所在直线的函数解析式; πr2h,其中r和h分别是圆锥的底面半)径和高).
πr2h,其中r和h分别是圆锥的底面半)径和高).
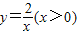 图象上一点,点A是线段OB上一点,以AB为半径作⊙A恰好与x轴、y轴分别切于点C和点D,则点A的坐标是 .
图象上一点,点A是线段OB上一点,以AB为半径作⊙A恰好与x轴、y轴分别切于点C和点D,则点A的坐标是 .