题目内容
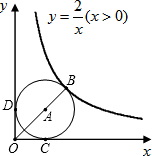 如图,点B是函数y=
如图,点B是函数y=| 2 | x |
分析:连接AC,AD,易证四边形OCAD为正方形,即可设点A的坐标为(a,a)(a>0),从而可得点B的横纵坐标相等,设点B的横坐标为x,即可得出x=
,故有OB=2,又OB=OA+AB,即2=a
+2,即可得出a的值,即A的坐标.
| 2 |
| 2 |
解答: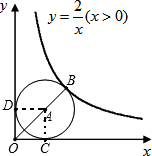 解:连接AC,AD,
解:连接AC,AD,
结合题意,可得四边形OCAD为正方形,
故点A和点B的横纵坐标均相等,
设A(a,a),B(x,x)
可得OA=a
,
又点B是函数y=
(x>0)图象上一点,
故可得出x=
,
即OB=2,
又OB=OA+a
即有2=a
+a
即a=2
-2
即A点的坐标为(2
-2,2
-2).
故答案为:(2
-2,2
-2).
 解:连接AC,AD,
解:连接AC,AD,结合题意,可得四边形OCAD为正方形,
故点A和点B的横纵坐标均相等,
设A(a,a),B(x,x)
可得OA=a
| 2 |
又点B是函数y=
| 2 |
| x |
故可得出x=
| 2 |
即OB=2,
又OB=OA+a
即有2=a
| 2 |
即a=2
| 2 |
即A点的坐标为(2
| 2 |
| 2 |
故答案为:(2
| 2 |
| 2 |
点评:本题主要考查了圆的切线的性质以及反比例函数的一般应用,通过求证四边形为正方形,得出点的横纵坐标之间的关系,以及两线段之间的数量关系,即可得出结果.

练习册系列答案
相关题目
 如图,点A是函数y=
如图,点A是函数y= 如图,点M是函数
如图,点M是函数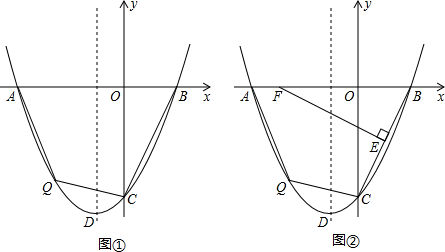
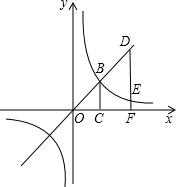 如图,点B是函数y=
如图,点B是函数y=