摘要: Ⅰ.证明:∵DEFG为正方形. ∴GD=FE.∠GDB=∠FEC=90° ∵△ABC是等边三角形.∴∠B=∠C=60° ∴△BDG≌△CEF(AAS) Ⅱa.解法一:设正方形的边长为x.作△ABC的高AH. 求得 由△AGF∽△ABC得: 解之得:(或) 解法二:设正方形的边长为x.则 在Rt△BDG中.tan∠B=. ∴ 解之得:(或) 解法三:设正方形的边长为x. 则 由勾股定理得: 解之得: Ⅱb.解: 正确 由已知可知.四边形GDEF为矩形 ∵FE∥F’E’ . ∴. 同理. ∴ 又∵F’E’=F’G’. ∴FE=FG 因此.矩形GDEF为正方形
网址:http://m.1010jiajiao.com/timu3_id_468175[举报]
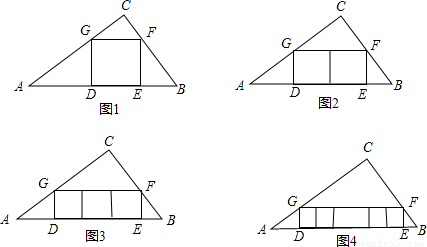
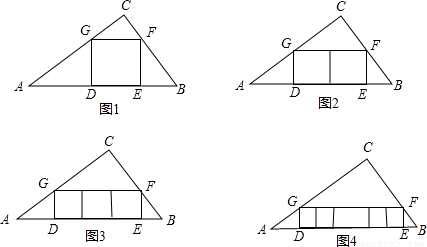
(根据课本习题改编)如图1,在△ABC中,∠C=90°,AC=4,BC=3,四边形DEFG为△ABC的内接正方形,若设正方形的边长为x,容易算出x的长为
.
探究与计算:
(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为 ;
(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为 ;
(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.
 查看习题详情和答案>>
查看习题详情和答案>>
| 60 | 37 |
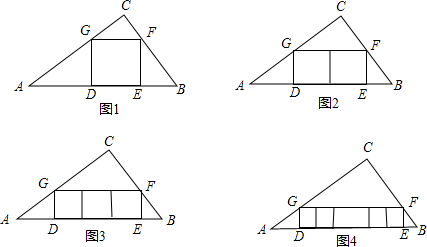
探究与计算:
(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为
(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为
(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.
 查看习题详情和答案>>
查看习题详情和答案>>
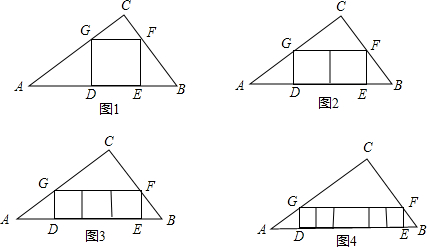
(根据课本习题改编)如图1,在△ABC中,∠C=90°,AC=4,BC=3,四边形DEFG为△ABC的内接正方形,若设正方形的边长为x,容易算出x的长为 .
.
探究与计算:
(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.
查看习题详情和答案>>
(根据课本习题改编)如图1,在△ABC中,∠C=90°,AC=4,BC=3,四边形DEFG为△ABC的内接正方形,若设正方形的边长为x,容易算出x的长为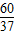 .
.
探究与计算:
(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.
查看习题详情和答案>>
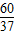 .
.探究与计算:
(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为______;
(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.

查看习题详情和答案>>

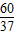 .
.