摘要： 解:原式= 当x=-1,y=时 原式=
网址：http://m.1010jiajiao.com/timu3_id_468144[举报]
解密码：
下面的六道题算式真是莫名其妙，但当你知道这是密码算式每个数字各自对应的是另一个不同数字时，事情就讲得通了，请你设法填出表中密码所对应的原来数字．
(1)8＋7＝62；(2)5＋3＝5；(3)12＋8＝23；(4)50＋9＝54；(5)11×1＝55；(6)0－9＝1
（原创题）如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为4个单位，点P从O点出发沿折线OAB向B点以2个单位/秒的
速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两点同时出发，运动时间为t（单位：秒）．
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t= 时，PQ⊥OA；当t= 时，PQ⊥AB；当t= 时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由． 查看习题详情和答案>>
速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两点同时出发，运动时间为t（单位：秒）．①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由． 查看习题详情和答案>>
（原创题）如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为4个单位，点P从O点出发沿折线OAB向B点以2个单位/秒的速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两点同时出发，运动时间为t（单位：秒）．
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=______时，PQ⊥OA；当t=______时，PQ⊥AB；当t=______时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由．
查看习题详情和答案>>
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=______时，PQ⊥OA；当t=______时，PQ⊥AB；当t=______时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由．
查看习题详情和答案>>
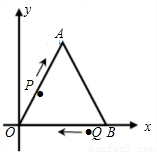
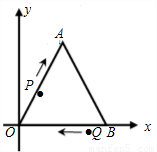
（原创题）如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为4个单位，点P从O点出发沿折线OAB向B点以2个单位/秒的速度向终点B点运动，点Q从B点出发以1个单位/秒的速度向终点O点运动，两点同时出发，运动时间为t（单位：秒）．
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=______时，PQ⊥OA；当t=______时，PQ⊥AB；当t=______时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由．
查看习题详情和答案>>
①直接写出P与Q点的坐标，并注明t的取值范围；
②当t=______时，PQ⊥OA；当t=______时，PQ⊥AB；当t=______时，PQ⊥OB；
③△OPQ面积为S，求S关于t的函数关系式并指出S的最大值；
④若直线PQ将△OAB分成面积比为3：5两部分，求此时直线PQ的解析式；若不能请说明理由．
查看习题详情和答案>>
