摘要： (1)证明:延长DC交BE于点M.∵BE∥AC.AB∥DC,∴四边形ABMC是平行四边形. ∴CM=AB=DC,C为DM的中点.BE∥AC.DF=FE; 得CF是△DME的中位线.故ME=2CF,又∵AC=2CF.四边形ABMC是平行四边形.∴BE=2BM=2ME=2AC, 又∵AC⊥DC, ∴在Rt△ADC中利用勾股定理得AC= , ∴=. (3)可将四边形ABED的面积分为两部分.梯形ABMD和三角形DME,在Rt△ADC中利用勾股定理得DC=,由CF是△DME的中位线得CM=DC=,四边形ABMC是平行四边形得AM=MC=,BM=AC=,∴梯形ABMD面积为:;由AC⊥DC和BE∥AC可证得三角形DME是直角三角形.其面积为:,∴四边形ABED的面积为+
网址：http://m.1010jiajiao.com/timu3_id_467738[举报]
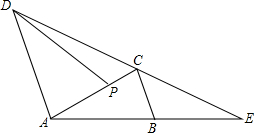
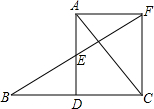如图，△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DC，连接CF．（1）求证：D是BC的中点；
（2）如果AB=AC，试猜想四边形ADCF的形状，并证明你的结论；
（3）△ABC满足什么条件时四边形ADCF为正方形，并证明你的结论．
如图，在
中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF＝DC，连接CF。
（1）求证：D是BC的中点；
（2）如果AB＝AC，试猜测四边形ADCF的形状，并证明你的结论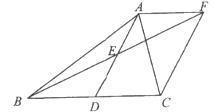
如图，在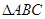
中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF＝DC，连接CF。
（1）求证：D是BC的中点；
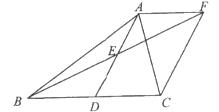
（2）如果AB＝AC，试猜测四边形ADCF的形状，并证明你的结论
查看习题详情和答案>>
，BA＝BC，BD⊥AC于D，E为DC上任意一点，AG⊥BE于G，交BD于F．
(BF＋DE)；
P=