摘要： (1)证明:分别过点C.D作 垂足为G.H.则 (2)①证明:连结MF.NE 设点M的坐标为.点N的坐标为. ∵点M.N在反比例函数的图象上. ∴. 由(1)中的结论可知:MN∥EF. ②MN∥EF.
网址：http://m.1010jiajiao.com/timu3_id_467657[举报]
一次函数
的图象分别与
轴、
轴交于点
，与反比例函数
的图象相交于点
．过点
分别作
轴，
轴，垂足分别为
；过点
分别作
轴，
轴，垂足分别为
与
交于点
，连接
．
（1）若点
在反比例函数的图象的同一分支上，如图1，试证明：
①
；
②
．
（2）若点分别在反比例函数的图象的不同分支上，如图2，则
与
还相等吗？试证明你的结论．
 |
查看习题详情和答案>>
一次函数
的图象分别与
轴、
轴交于点
，与反比例函数
的图象相交于点
．过点
分别作
轴，
轴，垂足分别为
；过点
分别作
轴，
轴，垂足分别为
与
交于点
，连接
．
（1）若点
在反比例函数的图象的同一分支上，如图1，试证明：
①
；
②
．
（2）若点分别在反比例函数的图象的不同分支上，如图2，则
与
还相等吗？试证明你的结论．
 |
查看习题详情和答案>>
已知：等边△ABC的边长为a，
探究（1）：如图1，过等边△ABC的顶点A、B、C依次作AB、BC、CA的垂线围成△MNG，求证：△MNG是等边三角形且MN=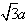
；
探究（2）：在等边△ABC内取一点O，过点O分别作OD⊥AB、OE⊥BC、OF⊥CA，垂足分别为点D、E、F。
①如图2，若点O是△ABC的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1：OD+OE+OF=
；结论2：AD+BE+CF=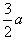
；
②如图3，若点O是等边△ABC内任意一点，则上述结论1，2是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由。
查看习题详情和答案>>
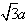；探究（2）：在等边△ABC内取一点O，过点O分别作OD⊥AB、OE⊥BC、OF⊥CA，垂足分别为点D、E、F。
①如图2，若点O是△ABC的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1：OD+OE+OF=
；结论2：AD+BE+CF=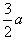；②如图3，若点O是等边△ABC内任意一点，则上述结论1，2是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由。
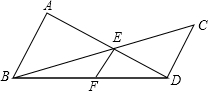
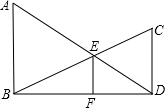已知：如图，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明