摘要: 解:解.得. 解.得.所以.原不等式组的解集是.
网址:http://m.1010jiajiao.com/timu3_id_466404[举报]
例:解不等式: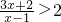
解:把不等式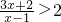 进行整理,得
进行整理,得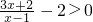 即
即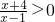 ,
,
则有 (1)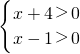 (2)
(2)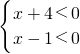
解不等式(1)得:x>1,解不等式(2)得:x<-4.
所以原不等式的解集是:x<-4 或x>1.
请根据以上解不等式的思想方法解不等式: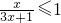 .
.
查看习题详情和答案>>
在解不等式|x+1|>2时,我们可以采用下面的解答方法:
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组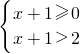
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=-(x+1).
∴由原不等式得-(x+1)>2.∴可得不等式组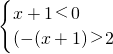
∴解得不等式组的解集为x<-3.
综上所述,原不等式的解集为x>1或x<-3.
请你仿照上述方法,尝试解不等式|x-2|≤1.
查看习题详情和答案>>
在解不等式|x+1|>2时,我们可以采用下面的解答方法:
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=-(x+1).
∴由原不等式得-(x+1)>2.∴可得不等式组
∴解得不等式组的解集为x<-3.
综上所述,原不等式的解集为x>1或x<-3.
请你仿照上述方法,尝试解不等式|x-2|≤1.
查看习题详情和答案>>
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组
|
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=-(x+1).
∴由原不等式得-(x+1)>2.∴可得不等式组
|
∴解得不等式组的解集为x<-3.
综上所述,原不等式的解集为x>1或x<-3.
请你仿照上述方法,尝试解不等式|x-2|≤1.
 如图所示,抛物线y=ax2+
如图所示,抛物线y=ax2+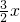 +c经过原点O和A(4,2),与x轴交于点C,点M、N同时从原点O出发,点M以2个单位/秒的速度沿y轴正方向运动,点N以1个单位/秒的速度沿x轴正方向运动,当其中一个点停止运动时,另一点也随之停止.
+c经过原点O和A(4,2),与x轴交于点C,点M、N同时从原点O出发,点M以2个单位/秒的速度沿y轴正方向运动,点N以1个单位/秒的速度沿x轴正方向运动,当其中一个点停止运动时,另一点也随之停止.