题目内容
在解不等式|x+1|>2时,我们可以采用下面的解答方法:
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组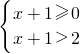
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=-(x+1).
∴由原不等式得-(x+1)>2.∴可得不等式组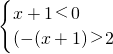
∴解得不等式组的解集为x<-3.
综上所述,原不等式的解集为x>1或x<-3.
请你仿照上述方法,尝试解不等式|x-2|≤1.
解:①当x-2≥0时,|x-2|=x-2.
∴由原不等式得x-2≤1.
∴可得不等式组 .
.
∴解得不等式组的解集为2≤x≤3.
②当x-2<0时,|x-2|=-(x-2).
∴由原不等式得-(x-2)≤1.
∴可得不等式组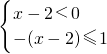 .
.
∴解得不等式组的解集为1≤x<2.
综上所述,原不等式的解集为1≤x≤3.
分析:分两种情况:①当x-2≥0时,|x-2|=x-2.②当x-2<0时,|x-2|=-(x-2).讨论即可求解.
点评:考查了含绝对值的一元一次不等式组,注意读懂题目的解答,以及分类思想的运用.
∴由原不等式得x-2≤1.
∴可得不等式组
 .
.∴解得不等式组的解集为2≤x≤3.
②当x-2<0时,|x-2|=-(x-2).
∴由原不等式得-(x-2)≤1.
∴可得不等式组
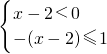 .
.∴解得不等式组的解集为1≤x<2.
综上所述,原不等式的解集为1≤x≤3.
分析:分两种情况:①当x-2≥0时,|x-2|=x-2.②当x-2<0时,|x-2|=-(x-2).讨论即可求解.
点评:考查了含绝对值的一元一次不等式组,注意读懂题目的解答,以及分类思想的运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
在解不等式
<
时,其中错误的一步是( )
①去分母得3(4x-1)<5(2-x);
②去括号得12x-3<10-5x;
③移项得12x+5<10+3;
④合并得17x<13;
⑤化系数为1得x<
.
| 1-4x |
| 5 |
| 2-x |
| -3 |
①去分母得3(4x-1)<5(2-x);
②去括号得12x-3<10-5x;
③移项得12x+5<10+3;
④合并得17x<13;
⑤化系数为1得x<
| 13 |
| 17 |
| A、① | B、② | C、③ | D、⑤ |
在解不等式
-
>1中指出最先出现错误的一步是( )
| x-1 |
| 2 |
| x+3 |
| 8 |
| A、4(x-1)-(x+3)>8 |
| B、4x-4-x+3>8 |
| C、3x>9 |
| D、x>3 |