摘要：如图10.在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA.OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根. (1)求C点的坐标, (2)以斜边AB为直径作圆与y轴交于另一点E.求过A.B.E三点的抛物线的解析式.并画出此抛物线的草图, (3)在抛物线上是否存在点P.使△ABP与△ABC全等?若存在.求出符合条件的P点的坐标,若不存在.说明理由.
网址：http://m.1010jiajiao.com/timu3_id_461567[举报]
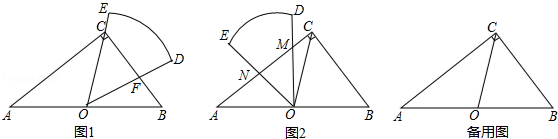
（2013•江宁区二模）根据三角形外心的概念，我们可引入如下概念：定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心．
（1）应用：如图1，PA=PB，过准外心P作PD⊥AB，垂足为D，PD=
AB，求∠PAD；
（2）探究：如图2，在Rt△ABC中，∠A=90°，BC=10，AB=6，准外心P在AC边上，试探究PA的长．
查看习题详情和答案>>
（1）应用：如图1，PA=PB，过准外心P作PD⊥AB，垂足为D，PD=
| ||
| 6 |
（2）探究：如图2，在Rt△ABC中，∠A=90°，BC=10，AB=6，准外心P在AC边上，试探究PA的长．
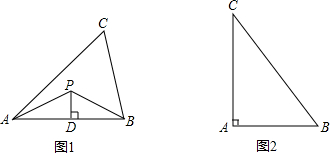
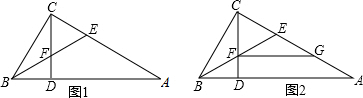
如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，作∠ABC的平分线交AC、CD于点E、F．
（1）求证：CE=CF；
（2）如图2，过点F作FG∥AB交AC于点G，若AC=10，EG=4，求CE的长度．
查看习题详情和答案>>
（1）求证：CE=CF；
（2）如图2，过点F作FG∥AB交AC于点G，若AC=10，EG=4，求CE的长度．
如图1，在Rt△ABC中，∠C=90°，BC=8cm，点D在AC上，CD=3cm．P，Q两点分别从A，C两点同时出发，点P沿AC向点C匀速运动，速度为每秒kcm，行完AC全程需8s；点Q沿CB向点B匀速运动，速度为每秒1cm．设运动的时间为xs（0＜x＜8），△DCQ的面积为y1cm2，△PCQ的面积为y2cm2．
（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）图2所示的抛物线是y2的图象，顶点坐标为（4，10），求图1中AB的长；
（3）在图2中，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别交y1，y2于点E，F．
①说出线段EF的长在图1中所表示的几何意义；
②P，Q两点在运动过程中，△PDQ的面积是否存在最大值？若存在，请求出点Q运动的时间和△PD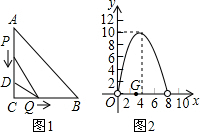
Q的最大面积；若不存在，请说明理由．
查看习题详情和答案>>
（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）图2所示的抛物线是y2的图象，顶点坐标为（4，10），求图1中AB的长；
（3）在图2中，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别交y1，y2于点E，F．
①说出线段EF的长在图1中所表示的几何意义；
②P，Q两点在运动过程中，△PDQ的面积是否存在最大值？若存在，请求出点Q运动的时间和△PD
Q的最大面积；若不存在，请说明理由．
查看习题详情和答案>>
