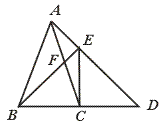
摘要:25.如图.在△ABC中.AB=AC.延长BC至D.使得CD=BC.CE⊥BD交AD于E.连结BE交AC于F.求证AF=FC. [提示]先证△BCF∽△DBA.再证=. [答案]∵ BC=CD.EC⊥BD. ∴ BE=DE.∠FBC=∠D. 又 AB=AC. ∴ ∠BCF=∠DBA. ∴ ∠BCF∽△DBA. ∴ =. 又 BD=2BC.AB=AC. ∴ ==. ∴ FC=AC. 因此 AF=FC.
网址:http://m.1010jiajiao.com/timu3_id_460749[举报]