摘要：6．如图.⊙O的弦AB.CD相交于点P.PA＝4厘米.PB＝3厘米.PC＝6厘米.EA切⊙O于点A.AE与CD的延长线交于点E.AE＝2厘米.则PE的长为( ) 3厘米 (C)厘米 (D)厘米 [提示]由相交弦定理.得PA·PB＝PD·PC． ∴ 4×3＝PD·6． ∴ PD＝2． 由切割线定理.得 AE2＝ED·EC． ∴ (2)2＝ED ·(ED+2+6)．解此方程得 ED＝2或ED＝-10． ∴ PE＝2+2＝4． [答案]A． [点评]本题考查相交弦定理.切割线定理．注意:应用相交弦定理.切割线定理往往建立方程.通过解方程求解．
网址：http://m.1010jiajiao.com/timu3_id_459628[举报]
如图，⊙O的弦AB、CD相交于点P，PA＝4厘米，PB＝3厘米，PC＝6厘米，EA切⊙O于点A，AE与CD的延长线交于点E，AE＝2
厘米，则PE的长为（ ）
（A）4厘米 （B）3厘米 （C）
厘米 （D）
厘米
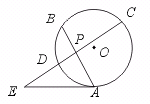
如图所示，⊙O的两条弦AB、CD相交于点E，AC和DB的延长线交于点P，则下列结论中成立的是
[ ]
A．PC·CA＝PB·BD
B．CE·AE＝BE·ED
C．CE·CD＝BE·BA
D．PB·PD＝PC·PA
查看习题详情和答案>>