Question

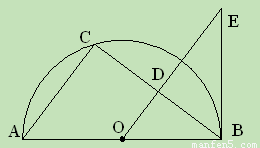
．(9分)如图，AB为⊙O内垂直于直径的弦，AB、CD相于点H，△AED与△AHD
关于直线AD成轴对称．
（1）试说明：AE为⊙O的切线；
（2）延长AE与CD交于点P，已知PA＝2，PD＝1，求⊙O的半径和DE的长．

Answer 1

（1）连结OA

由△AED与△AHD关于直线AD成轴对称可知∠ADO＝∠ADE  ………1分
因为AB⊥CD，所以∠AED＝∠AHD＝90°．
又因为OA＝OD，所以∠OAD＝∠ODA   …………………2分
所以∠OAD＝∠ADE，所以OA∥DE ………3分
所以∠OAP＝90°，又因为点A在圆上，所以AE为⊙O的切线．………4分
（2）设⊙O的半径为x,在Rt△AOP中，
OA²＋AP²＝OP²
x²＋2²＝(x＋1)²                      ………5分
解得x＝1.5

P

所以⊙O的半径为1.5        ………7分

因为OA∥DE，所以△PED∽△PAO
所以＝，＝，解得DE＝ ………9分

 解析:
略