摘要:25. 已知抛物线Y=x2+mx一2m2. (1)求证:该抛物线与X轴有两个不同的交点, 作Y轴的垂线交该抛物线于点A和点B.是 否存在实数m.n.使得AP=2PB?若存在.则求出m.n满足的条件,若不存在. 请说明理由. 数学试卷第4页
网址:http://m.1010jiajiao.com/timu3_id_458813[举报]
已知抛物线的顶点为y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA),B(0,yB),C(-1,yC)在该抛物线上,当y0≥0恒成立时,
的最小值为( )
| yA |
| yB-yC |
| A、1 | B、2 | C、4 | D、3 |
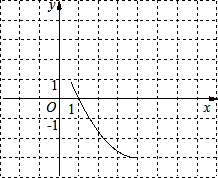 已知抛物线y=
已知抛物线y=| 1 |
| 3 |
| A、(5,0) |
| B、(6,0) |
| C、(7,0) |
| D、(0,7) |
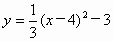 的部分图像如图所示,图像再次与x轴相交时的坐标是
的部分图像如图所示,图像再次与x轴相交时的坐标是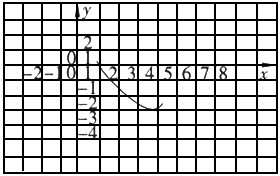
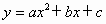 经过点(1,2)与(-1,4),则a+c的值是________.
经过点(1,2)与(-1,4),则a+c的值是________.