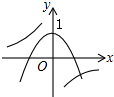
题目内容
已知抛物线的顶点为y=ax2+bx+c（0＜2a＜b）的顶点为P（x0，y0），点A（1，yA），B（0，yB），C（-1，yC）在该抛物线上，当y0≥0恒成立时，
的最小值为（ ）
| yA |
| yB-yC |
| A、1 | B、2 | C、4 | D、3 |
练习册系列答案
相关题目
在一个口袋中有4个完全相同的小球，把它们分别标号为①，②，③，④，随机地摸出一个小球，记录后放回，再随机摸出一个小球，则两次摸出的小球的标号相同的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
对于二次函数y=（x-1）2+2的图象，下列说法正确的是（ ）
| A、开口向下 | B、对称轴是x=-1 | C、顶点坐标是（1，2） | D、与x轴有两个交点 |
下列函数中，当x＞0时，y值随x值的增大而减小的是（ ）
| A、y=x | ||
| B、y=2x-1 | ||
C、y=
| ||
| D、y=x2 |
若二次函数y=ax2-2x+a2-4（a为常数）的图象如图，则该图象的对称轴是（ ）| A、直线x=-1 | ||
| B、直线x=1 | ||
C、直线x=-
| ||
D、直线x=
|
抛物线y=
(x-2)2-3的顶点坐标是（ ）
| 1 |
| 2 |
| A、（2，3） |
| B、（2，-3） |
| C、（-2，3） |
| D、（-2，-3） |
抛物线y=-（x+1）2+3的顶点坐标是（ ）
| A、（-1，-3） | B、（1，-3） | C、（-1，3） | D、（1，3） |
如图，二次函数y=x2+（2-m）x+m-3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（ ）| A、m＞2 | B、m＜3 | C、m＞3 | D、2＜m＜3 |