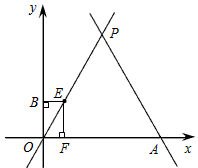摘要:已知:如图.直线y=-x+3与x轴.y轴分别交于点B.C.抛物线y=-x2+bx+c经过点B.C.点A是抛物线与x轴的另一个交点. (1)求抛物线的解析式. (2)若点P在直线BC上.且S△PAC=S△PAB.求点P的坐标.
网址:http://m.1010jiajiao.com/timu3_id_458718[举报]
已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2, ).
).
(1)请判断 的形状并说明理由.
的形状并说明理由.
(2)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥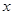 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值
 已知:如图,直线
已知:如图,直线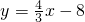 与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.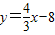 与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2,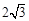 ).
).
 的形状并说明理由.
的形状并说明理由. 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S. 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P。
相交于点P。