题目内容
已知:如图,直线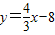 与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
【答案】分析:因为直线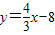 与X轴、Y轴分别交于A、B两点,所以分别令y=0,x=0即可求出A(6,0)、B(0,-8),由勾股定理可得AB=10,又因I是△AOB的内心,所以I到三角形各边的距离相等,因此过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是正方形,并且IM=IN=
与X轴、Y轴分别交于A、B两点,所以分别令y=0,x=0即可求出A(6,0)、B(0,-8),由勾股定理可得AB=10,又因I是△AOB的内心,所以I到三角形各边的距离相等,因此过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是正方形,并且IM=IN=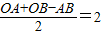 ,所以可求I的坐标为(2,-2),然后可设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得到一个方程组,解之即可求解.
,所以可求I的坐标为(2,-2),然后可设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得到一个方程组,解之即可求解.
解答: 解:直线
解:直线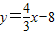 与X轴、Y轴分别交于A、B两点,
与X轴、Y轴分别交于A、B两点,
∴A(6,0)、B(0,-8),由勾股定理得AB=10.
∵I是△AOB的内心,过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是
正方形,IM=IN=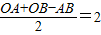 .
.
∴I的坐标为(2,-2).
设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得:
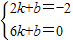 .解得k=
.解得k= ,b=-3.
,b=-3.
故直线AI的解析式为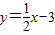 .
.
点评:本题需利用直角三角形的内心的性质求出该内心的坐标,结合待定系数法即可解决问题.
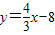 与X轴、Y轴分别交于A、B两点,所以分别令y=0,x=0即可求出A(6,0)、B(0,-8),由勾股定理可得AB=10,又因I是△AOB的内心,所以I到三角形各边的距离相等,因此过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是正方形,并且IM=IN=
与X轴、Y轴分别交于A、B两点,所以分别令y=0,x=0即可求出A(6,0)、B(0,-8),由勾股定理可得AB=10,又因I是△AOB的内心,所以I到三角形各边的距离相等,因此过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是正方形,并且IM=IN=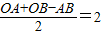 ,所以可求I的坐标为(2,-2),然后可设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得到一个方程组,解之即可求解.
,所以可求I的坐标为(2,-2),然后可设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得到一个方程组,解之即可求解.解答:
 解:直线
解:直线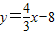 与X轴、Y轴分别交于A、B两点,
与X轴、Y轴分别交于A、B两点,∴A(6,0)、B(0,-8),由勾股定理得AB=10.
∵I是△AOB的内心,过I作IM⊥X轴,IN⊥Y轴可得四边形IMON是
正方形,IM=IN=
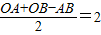 .
.∴I的坐标为(2,-2).
设直线AI的解析式为y=kx+b(k≠0)将I(2,-2)和A(6,0)代入得:
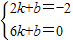 .解得k=
.解得k= ,b=-3.
,b=-3.故直线AI的解析式为
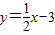 .
.点评:本题需利用直角三角形的内心的性质求出该内心的坐标,结合待定系数法即可解决问题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 已知:如图,直线与两坐标轴相交于A、B两点,
已知:如图,直线与两坐标轴相交于A、B两点,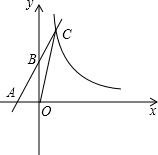 已知,如图,直线
已知,如图,直线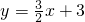 与x轴、y轴分别相交于A、B两点,与双曲线
与x轴、y轴分别相交于A、B两点,与双曲线 在第一象限内交于点C,且S△AOC=9.求反比例函数的解析式.
在第一象限内交于点C,且S△AOC=9.求反比例函数的解析式. 已知:如图,直线
已知:如图,直线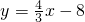 与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式.
与X轴、Y轴分别交于A、B两点,△ABO的内心为I,求:直线AI的解析式. 与双曲线
与双曲线 (k>0)交于A、B两点,点A、B的横坐标之比为1:3,则k= .
(k>0)交于A、B两点,点A、B的横坐标之比为1:3,则k= .
 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.
与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.