摘要:(1)过A作ACBF.垂足为C 在RTABC中 AB=300km (2) 答:A城遭遇这次台风影响10个小时.
网址:http://m.1010jiajiao.com/timu3_id_458213[举报]
如图,已知直线y=-
x+2
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.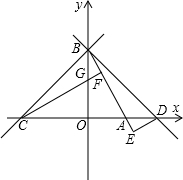
(1)求C点的坐标;
(2)若将△OBC沿y轴翻折,C点落在x轴上的D点,过D作DE⊥BA垂足为E,过C作CF⊥BA垂足为F,交BO于G,试说明AE与FG的数量关系;
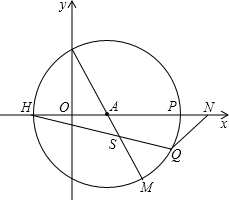
(3)以A点为圆心,以AB为半径作⊙A交x轴负半轴于点H,交x轴正半轴于点P,BA的延长线交⊙A于M,在
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
 查看习题详情和答案>>
查看习题详情和答案>>
| 3 |
| 3 |

(1)求C点的坐标;
(2)若将△OBC沿y轴翻折,C点落在x轴上的D点,过D作DE⊥BA垂足为E,过C作CF⊥BA垂足为F,交BO于G,试说明AE与FG的数量关系;
(3)以A点为圆心,以AB为半径作⊙A交x轴负半轴于点H,交x轴正半轴于点P,BA的延长线交⊙A于M,在
 |
| PM |
 查看习题详情和答案>>
查看习题详情和答案>>
如图1,正方形ABCD和过其对角线交点O的正方形OEFG的边长相等,OE交AB于M,OG交BC于N.
(1)求证:△AOM≌△BON;
(2)当四边形MONB的面积为1时,求正方形的边长;
(3)在(2)的条件下,如果正方形OEFG绕点O逆时针转动,使顶点E刚好落在CB的延长线上如图2,并过O作OH⊥BC垂足为H,求MB的长.

查看习题详情和答案>>
(1)求证:△AOM≌△BON;
(2)当四边形MONB的面积为1时,求正方形的边长;
(3)在(2)的条件下,如果正方形OEFG绕点O逆时针转动,使顶点E刚好落在CB的延长线上如图2,并过O作OH⊥BC垂足为H,求MB的长.

(本小题满分10分)如图,已知抛物线经过A(-2,0),B(-3,3) 及原点 ,顶点为
,顶点为 .
.
(1)求抛物线的解析式;
(2)若点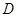 在抛物线上,点
在抛物线上,点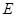 在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)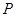 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点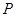 作
作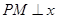 轴,垂足为
轴,垂足为 ,是否存在点
,是否存在点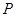 ,使得以
,使得以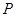 、
、 、
、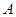 为顶点的三角形与
为顶点的三角形与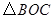 相似?若存在,求出点
相似?若存在,求出点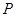 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

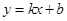 的图像与反比例函数
的图像与反比例函数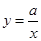 的图像交于
的图像交于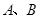 两点,与
两点,与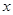 轴交于点
轴交于点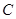 ,与
,与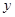 轴交于点
轴交于点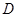 ,已知
,已知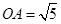 ,点
,点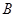 的坐标为
的坐标为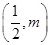 ,过点
,过点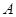 作
作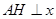 轴,垂足为
轴,垂足为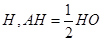
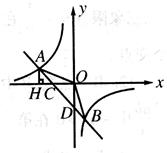
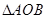 的面积
的面积