摘要:解:过A作ADBC.垂足为D. (4)实例分析
网址:http://m.1010jiajiao.com/timu3_id_458207[举报]
如图1,正方形ABCD和过其对角线交点O的正方形OEFG的边长相等,OE交AB于M,OG交BC于N.
(1)求证:△AOM≌△BON;
(2)当四边形MONB的面积为1时,求正方形的边长;
(3)在(2)的条件下,如果正方形OEFG绕点O逆时针转动,使顶点E刚好落在CB的延长线上如图2,并过O作OH⊥BC垂足为H,求MB的长.

查看习题详情和答案>>
(1)求证:△AOM≌△BON;
(2)当四边形MONB的面积为1时,求正方形的边长;
(3)在(2)的条件下,如果正方形OEFG绕点O逆时针转动,使顶点E刚好落在CB的延长线上如图2,并过O作OH⊥BC垂足为H,求MB的长.

25、阅读下列解题过程:
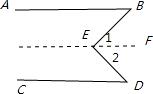
如图,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:过E作EF∥AB,则AB∥CD∥EF(平行的传递性)
AB∥EF?∠B=∠1=35°
又因为CD∥EF?∠D=∠2=32°
所以∠BED=∠BED=∠1+∠235°+32°=67°(等量代换)
然后解答下列问题:
如图,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决:
问题(1):∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A=
问题(2):∠G+∠F+∠H=

查看习题详情和答案>>
如图,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:过E作EF∥AB,则AB∥CD∥EF(平行的传递性)
AB∥EF?∠B=∠1=35°
又因为CD∥EF?∠D=∠2=32°
所以∠BED=∠BED=∠1+∠235°+32°=67°(等量代换)
然后解答下列问题:
如图,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决:
问题(1):∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A=
35°
;问题(2):∠G+∠F+∠H=
360
°时,GP∥HQ.

如图,已知直线y=-
x+2
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.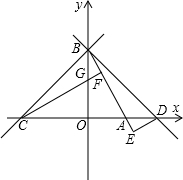
(1)求C点的坐标;
(2)若将△OBC沿y轴翻折,C点落在x轴上的D点,过D作DE⊥BA垂足为E,过C作CF⊥BA垂足为F,交BO于G,试说明AE与FG的数量关系;
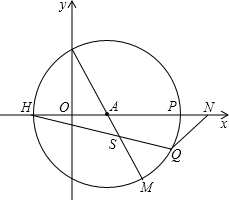
(3)以A点为圆心,以AB为半径作⊙A交x轴负半轴于点H,交x轴正半轴于点P,BA的延长线交⊙A于M,在
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
 查看习题详情和答案>>
查看习题详情和答案>>
| 3 |
| 3 |

(1)求C点的坐标;
(2)若将△OBC沿y轴翻折,C点落在x轴上的D点,过D作DE⊥BA垂足为E,过C作CF⊥BA垂足为F,交BO于G,试说明AE与FG的数量关系;
(3)以A点为圆心,以AB为半径作⊙A交x轴负半轴于点H,交x轴正半轴于点P,BA的延长线交⊙A于M,在
 |
| PM |
 查看习题详情和答案>>
查看习题详情和答案>>
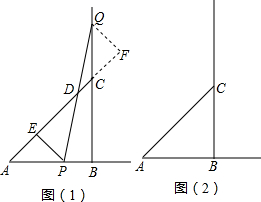 (1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.①当点P在线段AB上运动时,线段DE的长度是否改变?若不改变,求出DE的值;若改变,请说明理由.
下面给出一种解题的思路,你可以按这一思路解题,也可以选择另外的方法解题.
解:过Q作QF⊥直线AC于点M
∵PE⊥AC于点E,QF⊥直线AC于点M
∴∠AEP=∠F=90°
(下面请你完成余下的解题过程)
②当点P在线段AB的延长线上运动时,(1)中的结论是否还成立?请在图2画出图形并说明理由.
(2)若将(1)中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时(其余条件不变),则线段DE的长度又如何?(直接写出答案,不需要解题过程)
(3)若将(2)中的“等边△ABC”改为“△ABC”(其余条件不变),请你做出猜想:当△ABC满足
∠A=∠ACB
∠A=∠ACB
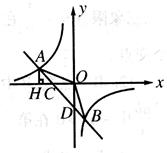
条件时,(2)中的结论仍然成立.(直接写出答案,不需要解题过程)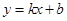 的图像与反比例函数
的图像与反比例函数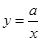 的图像交于
的图像交于 两点,与
两点,与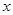 轴交于点
轴交于点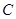 ,与
,与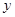 轴交于点
轴交于点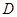 ,已知
,已知 ,点
,点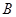 的坐标为
的坐标为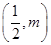 ,过点
,过点 作
作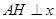 轴,垂足为
轴,垂足为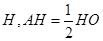
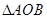 的面积
的面积