摘要: 已知:如图1.在△ABC中 .AB = AC =5 .AD为底边BC上的高.且AD = 3.将△ACD沿箭头所示的方向平移.得到△A'CD'.A'D' 交AB于E.A'C分别交AB.AD 于G.F.以 D'D 为直径作⊙O.设BD'的长为 x .⊙O的面积为 y . (1)求 y与x 的函数关系式及自变量x的取值范围, (2)当BD'的长为多少时.⊙O的面积与△ABD的面积相等? (3)连结EF.求EF与⊙O 相切时 x 的值. [解]:(1) (2) (3)
网址:http://m.1010jiajiao.com/timu3_id_457749[举报]
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.

1.(1)求证:AC=3BF;
2.(2)如果![]() ,求证:
,求证:![]() .
.
查看习题详情和答案>>
(本题满分12分)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF= 90°,∠DEF = 45°,AC =6cm,BC = 6 cm,EF = 12cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)当t为何值时,△PQE是直角三角形?
(3)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(4)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由
查看习题详情和答案>>
(本题满分12分 第(1)小题6分,第(2)小题6分)
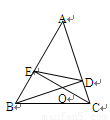
已知:如图,在△ABC中,BD⊥AC于点D, CE⊥AB于点E,EC和BD相交于点O,联接DE. 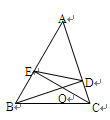
(1)求证:△EOD∽△BOC;
(2)若S△EOD=16,S△BOC=36,求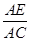 的值.
的值.
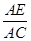 的值.
的值.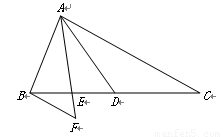
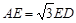 ,求证:
,求证: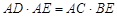 .
.