网址：http://m.1010jiajiao.com/timu3_id_457671[举报]
借助东、南、西、北的方位，用射线来表示方向，我们常称这种角叫做方位角．这种方位角表示有一定的要求：第一个字先写南或北(即以南、北为基准)，然后再写偏东或偏西多少度．如图，射线OA表示的方向是北偏东30°(注意：不能写成东偏北60°)，射线OB表示的方向是南偏西60°(注意：不能写成西偏南30°)．特别地，当射线为四个直角的角平分线时，分别称：东北方向，西北方向，西南方向，东南方向．考察队从A地出发，沿北偏东60°方向前进了5 km到达B地，再沿东南方向前进到C地，C地正好在A的正东方向．
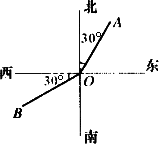
(1)按1∶200 000的比例画出考察队行进路线图．
(2)测量∠ABC和∠BCA的度数．
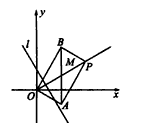
出发，沿射线OM方向以每秒1个单位长度的速度做匀速运动，在运动过程中，以OP为对角线的矩形OAPB的边长OA∶OB=
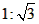，过点O且垂直于射线OM的直线l与点P同时出发，且与点P沿相同的方向、以相同的速度运动。（1）在点P运动过程中，试判断AB与y轴的位置关系，并说明理由；
（2）设点P与直线l都运动了t秒，求此时的矩形OAPB与直线l在运动过程中所扫过区域的重叠部分的面积S（用含t的代数式表示）。
操作与探索：
已知点O为直线AB上一点，作射线OC，将直角三角板ODE放置在直线上方(如图①)，使直角顶点与点O重合，一条直角边OD重叠在射线OA上，将三角板绕点O旋转
（1）当三角板旋转到如图②的位置时，若OD平分∠AOC，试说明OE也平分∠BOC.
（2）若OC⊥AB，垂足为点O(如图③)，请直接写出与∠DOB互补的角
（3）若∠AOC=135°(如图④)，三角板绕点O按顺时针从如图①的位置开始旋转，到OE边与射线OB重合结束. 请通过操作，探索：在旋转过程中，∠DOB
∠COE的差是否发生变化？若不变，请求出这个差值；若变化，请用含有n(n为三角板旋转的度数)的代数式表示这个差.
操作与探索：
已知点O为直线AB上一点，作射线OC，将直角三角板ODE放置在直线上方(如图①)，使直角顶点与点O重合，一条直角边OD重叠在射线OA上，将三角板绕点O旋转
（1）当三角板旋转到如图②的位置时，若OD平分∠AOC，试说明OE也平分∠BOC.
（2）若OC⊥AB，垂足为点O(如图③)，请直接写出与∠DOB互补的角
（3）若∠AOC=135°(如图④)，三角板绕点O按顺时针从如图①的位置开始旋转，到OE边与射线OB重合结束. 请通过操作，探索：在旋转过程中，∠DOB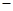
∠COE的差是否发生变化？若不变，请求出这个差值；若变化，请用含有n(n为三角板旋转的度数)的代数式表示这个差.
查看习题详情和答案>>
已知点O为直线AB上一点，作射线OC，将直角三角板ODE放置在直线上方(如图①)，使直角顶点与点O重合，一条直角边OD重叠在射线OA上，将三角板绕点O旋转
（1）当三角板旋转到如图②的位置时，若OD平分∠AOC，试说明OE也平分∠BOC.
（2）若OC⊥AB，垂足为点O(如图③)，请直接写出与∠DOB互补的角
（3）若∠AOC=135°(如图④)，三角板绕点O按顺时针从如图①的位置开始旋转，到OE边与射线OB重合结束. 请通过操作，探索：在旋转过程中，∠DOB
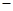∠COE的差是否发生变化？若不变，请求出这个差值；若变化，请用含有n(n为三角板旋转的度数)的代数式表示这个差.